Home » Subject » Graph Theory » Basic G.T.
Importance: High ✭✭✭
Author(s): Alon, Noga
Mubayi, Dhruv
Subject: Graph Theory
» Basic Graph Theory
Keywords: regular
subgraph
Recomm. for undergrads: no
Posted by: mdevos
on: May 22nd, 2008
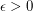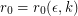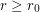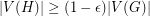Conjecture   For every $ \epsilon > 0 $ and every positive integer $ k $, there exists $ r_0 = r_0(\epsilon,k) $ so that every simple $ r $-regular graph $ G $ with $ r \ge r_0 $ has a $ k $-regular subgraph $ H $ with $ |V(H)| \ge (1- \epsilon) |V(G)| $.

Petersen's theorem asserts that every regular graph of even degree contains a 2-factor (i.e. a spanning 2-regular subgraph). Iterating this easy result we find that for any pair of positive even integers 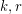$ k,r $, every $ r $-regular graph has a spanning $ k $-regular subgraph. The cases when either $ k $ or $ r $ is odd are considerably more complicated. There are some nice general results (see [AFK]) which show that every regular graph of sufficiently high degree contains a $ k $-regular subgraph. However these theorems give no bound on the size of this subgraph.

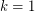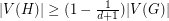For $ k=1 $ this conjecture is an easy consequence of Vizing's Theorem. Indeed, this theorem implies that every $ d $-regular graph $ G $ has a 1-regular subgraph $ H $ with $ |V(H)| \ge (1 - \frac{1}{d+1}) |V(G)| $ (just choose a largest color class from a 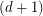$ (d+1) $-edge coloring). Alon [A] proved the conjecture for 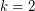$ k=2 $ with the help of two famous results on permanents: the Minc Conjecture (proved by Bregman), and the van der Waerden conjecture (proved by Falikman and Egorichev). It is open for all $ k \ge 3 $.

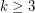Bibliography

*[A] N. Alon, Problems and results in extremal combinatorics, J, Discrete Math. 273 (2003), 31-53.

[AFK] N. Alon, S. Friedland and G. Kalai, Regular subgraphs of almost regular graphs, J. Combinatorial Theory, Ser. B 37(1984), 79-91.


* indicates original appearance(s) of problem.
add new comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options