 login/create account
login/create account
Is there an algorithm to determine if a triangulated 4-manifold is combinatorially equivalent to the 4-sphere?
A 4-manifold triangulation admits a unique smoothing up to diffeomorphism, so this problem is equivalent to asking for an algorithm to determine if a 4-manifold is diffeomorphic to the 4-sphere (with standard differentiable structure). "Combinatorial equivalence" refers to the ability to pass from one triangulation to another via a sequence of Pachner moves.
Rubinstein has an algorithm to determine if a triangulated 3-manifold is combinatorially equivalent to the 3-sphere. A consequence of his algorithm is that there is an algorithm to determine if a 4-dimensional simplicial complex is a 4-manifold triangulation.
It's known that no algorithms exist to determine if a triangulated 4-manifold has a trivial fundamental group, as there is a procedure to construct a compact 4-manifold with any finitely presented fundamental group.
In dimensions 5 and higher, Novikov proved that there is no algorithm to decide whether a given triangulated  -manifold is combinatorially equivalent to the
-manifold is combinatorially equivalent to the  -sphere is undecidable [N, CL]. Also, it is undecidable whether a given triangulated 4-manifold is combinatorially equivalent to a connect sum of 14 copies of
-sphere is undecidable [N, CL]. Also, it is undecidable whether a given triangulated 4-manifold is combinatorially equivalent to a connect sum of 14 copies of 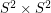 .
.
Bibliography
[CL] Chernavsky, A. V, and Leskine, V. P., Unrecognizability of manifolds, Annals of Pure and Applied Logic 141 (2006) 325--335.
[N] Novikov, P.S., On the algorithSSSR 85 (5) (19552) 709--712 (in Russian). Algorithmic unsolvability of the problem of identity, Dokl. Akad. Nauk SSSR 85 (5) (1952) 709--712 (in Russian).
[T] Thompson, A. Thin position and the recognition problem for 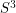 . MRL (1994).
. MRL (1994).
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University