 login/create account
login/create account
Smooth 4-dimensional Poincare conjecture
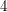 -manifold has the homotopy type of the
-manifold has the homotopy type of the 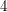 -sphere
-sphere 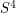 , is it diffeomorphic to
, is it diffeomorphic to 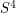 ?
?
The original Poincare conjecture was the assertion that a simply-connected compact boundaryless 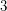 -manifold is diffeomorphic (smooth Poincare conjecture) or homeomorphic (topological Poincare conjecture) to
-manifold is diffeomorphic (smooth Poincare conjecture) or homeomorphic (topological Poincare conjecture) to 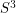 . Because of Poincare duality, this is equivalent to the assertion that a
. Because of Poincare duality, this is equivalent to the assertion that a 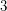 -manifold has the homotopy-type of
-manifold has the homotopy-type of 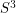 then it is diffeomorphic/homeomorphic to
then it is diffeomorphic/homeomorphic to 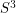 . This gave birth to the generalized Poincare conjecture -- that an
. This gave birth to the generalized Poincare conjecture -- that an  -manifold with the homotopy type of
-manifold with the homotopy type of 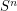 is diffeomorphic or homeomorphic to
is diffeomorphic or homeomorphic to 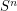 .
.
By the work of Smale and Stallings, the topological Poincare conjecture was shown to be true provided 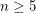 . But for
. But for 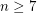 Milnor and Kervaire showed that
Milnor and Kervaire showed that 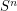 admits non-standard smooth structures so the smooth Poincare conjecture is false in general.
admits non-standard smooth structures so the smooth Poincare conjecture is false in general.
The generalized Poincare conjecture is an undergraduate-level point-set topology problem for 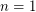 .
.
The 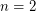 case was proven by Poincare.
case was proven by Poincare.
The 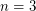 case was recently proven by Perelman.
case was recently proven by Perelman.
The 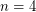 case is the only outstanding case. Mike Freedman has proven that a
case is the only outstanding case. Mike Freedman has proven that a 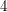 -manifold which is homotopy-equivalent to
-manifold which is homotopy-equivalent to 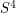 is homeomorphic to
is homeomorphic to 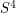 , so the smooth 4-dimensional Poincare conjecture is the only outstanding problem among the generalized Poincare conjectures. Moreover, it can be considered to be reduced to the question of if
, so the smooth 4-dimensional Poincare conjecture is the only outstanding problem among the generalized Poincare conjectures. Moreover, it can be considered to be reduced to the question of if 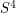 has an exotic smooth structure.
has an exotic smooth structure.
Technically, Poincare never asserted this conjecture. He only stated it was an interesting problem. So perhaps it should be called Poincare's Egregious Problem.
It is unknown whether or not 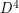 admits an exotic smooth structure. If not, the smooth
admits an exotic smooth structure. If not, the smooth 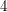 -dimensional Poincare conjecture would have an affirmative answer. Similarly, it's known that
-dimensional Poincare conjecture would have an affirmative answer. Similarly, it's known that 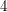 -dimensional euclidean space
-dimensional euclidean space 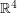 admits a continuum of pairwise non-diffeomorphic smooth structures. But it's unknown whether or not any of these exotic smooth structures extend to
admits a continuum of pairwise non-diffeomorphic smooth structures. But it's unknown whether or not any of these exotic smooth structures extend to 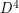 , thought of as a compactification of
, thought of as a compactification of 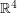 .
.
Bibliography
[FQ] Freedman, M. Quinn, F. Topology of 4-manifolds. Princeton University Press.
[S] Smale, S., "On the structure of manifolds" Amer. J. Math. , 84 (1962) pp. 387–399
[MT] Morgan, John W.; Gang Tian. Ricci Flow and the Poincaré Conjecture. AMS/CMI (2009)
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
Poincare conj is true in some dimensions > 7.
For n equals 12, 56 and 61, Sn also has a unique smooth structure.