 login/create account
login/create account
Smooth 4-dimensional Schoenflies problem
 be a
be a  -dimensional smooth submanifold of
-dimensional smooth submanifold of  ,
,  diffeomorphic to
diffeomorphic to 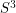 . By the Jordan-Brouwer separation theorem,
. By the Jordan-Brouwer separation theorem,  separates
separates  into the union of two compact connected
into the union of two compact connected  -manifolds which share
-manifolds which share  as a common boundary. The Schoenflies problem asks, are these
as a common boundary. The Schoenflies problem asks, are these  -manifolds diffeomorphic to
-manifolds diffeomorphic to 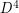 ? ie: is
? ie: is  unknotted?
unknotted? By the work of Mike Freedman,  separates
separates  into two manifolds which are homeomorphic to
into two manifolds which are homeomorphic to 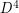 . So the Schoenflies problem is only non-trivial if
. So the Schoenflies problem is only non-trivial if 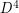 admits an exotic smooth structure, which is also an open problem. Although
admits an exotic smooth structure, which is also an open problem. Although 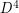 could very well have an exotic smooth structure and yet the Schoenflies problem could have a positive answer. ie: although exotic smooth
could very well have an exotic smooth structure and yet the Schoenflies problem could have a positive answer. ie: although exotic smooth 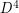 's might exist, perhaps none of them embed in
's might exist, perhaps none of them embed in  ?
?
Martin Scharlemann has results to the effect that the Schoenflies problem is true provided the embeddings are simple enough.
The smooth Poincare conjecture in dimension 4 is related but disjoint from this problem. For example, the Poincare conjecture could be true and 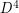 could have an exotic smooth structure -- this would amount to saying the monoid of smooth homotopy 4-spheres has some elements with inverses.
could have an exotic smooth structure -- this would amount to saying the monoid of smooth homotopy 4-spheres has some elements with inverses.
The analogous problem in other dimensions is known to be true. Namely, all embeddings of 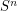 in
in 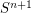 are unknotted (bound manifolds diffeomorphic to
are unknotted (bound manifolds diffeomorphic to 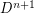 ) provided
) provided 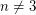 . For
. For 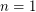 this is due to Schoenflies. For
this is due to Schoenflies. For 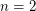 it's due to Alexander (see Hatcher's 3-manifolds notes for a modern exposition). For
it's due to Alexander (see Hatcher's 3-manifolds notes for a modern exposition). For 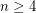 the result follows from the combination of the Mazur-Brown theorem that an embedding of
the result follows from the combination of the Mazur-Brown theorem that an embedding of 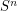 in
in 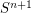 bounds a manifold homeomorphic to
bounds a manifold homeomorphic to 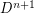 , plus a consequence of the H-cobordism theorem which states that
, plus a consequence of the H-cobordism theorem which states that 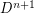 has no exotic smooth structures which restrict to the standard smooth structure on the boundary, provided
has no exotic smooth structures which restrict to the standard smooth structure on the boundary, provided 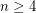 .
.
Bibliography
*[A] Alexander, J, On the subdivision of space by a polyhedron. Proc. Nat. Acad. Sci. USA 10 (1924) pg 6--8.
[FQ] Freedman, M. Quinn, F. Topology of 4-manifolds. Princeton University Press.
[S1] Scharlemann, M. The four-dimensional Schoenflies conjecture is true for genus two imbeddings. Topology 23 (1984) 211-217.
[S2] Scharlemann, M. Smooth Spheres in R4 with four critical points are standard. Inventiones Math. 79 (1985) 125-141.
[S3] Scharlemann, M. Generalized Property R and the Schoenflies Conjecture, Commentarii Mathematici Helvetici, 83 (2008) 421--449.
[MMEB] Marston Morse and Emilio Baiada, Homotopy and Homology Related to the Schoenflies Problem. The Annals of Mathematics, Second Series, Vol. 58, No. 1 (Jul., 1953), pp. 142-165
[B] Brown, Morton. A proof of the generalized Schoenflies theorem. Bull. Amer. Math. Soc., vol. 66, pp. 74–76. (1960)
[MAZ] Mazur, Barry, On embeddings of spheres., Bull. Amer. Math. Soc. 65 (1959) 59--65.
[H] Hatcher, A. 3-manifolds notes. [http://www.math.cornell.edu/~hatcher/3M/3Mdownloads.html]
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University