 login/create account
login/create account
Alexander, J
Smooth 4-dimensional Schoenflies problem ★★★★
Author(s): Alexander
Problem Let  be a
be a  -dimensional smooth submanifold of
-dimensional smooth submanifold of  ,
,  diffeomorphic to
diffeomorphic to 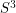 . By the Jordan-Brouwer separation theorem,
. By the Jordan-Brouwer separation theorem,  separates
separates  into the union of two compact connected
into the union of two compact connected  -manifolds which share
-manifolds which share  as a common boundary. The Schoenflies problem asks, are these
as a common boundary. The Schoenflies problem asks, are these  -manifolds diffeomorphic to
-manifolds diffeomorphic to 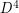 ? ie: is
? ie: is  unknotted?
unknotted?
 be a
be a  -dimensional smooth submanifold of
-dimensional smooth submanifold of  ,
,  diffeomorphic to
diffeomorphic to 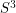 . By the Jordan-Brouwer separation theorem,
. By the Jordan-Brouwer separation theorem,  separates
separates  into the union of two compact connected
into the union of two compact connected  -manifolds which share
-manifolds which share  as a common boundary. The Schoenflies problem asks, are these
as a common boundary. The Schoenflies problem asks, are these  -manifolds diffeomorphic to
-manifolds diffeomorphic to 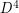 ? ie: is
? ie: is  unknotted?
unknotted? Keywords: 4-dimensional; Schoenflies; sphere

 Drupal
Drupal CSI of Charles University
CSI of Charles University