 login/create account
login/create account
4-sphere
Is there an algorithm to determine if a triangulated 4-manifold is combinatorially equivalent to the 4-sphere? ★★★
Author(s): Novikov
Problem Is there an algorithm which takes as input a triangulated 4-manifold, and determines whether or not this manifold is combinatorially equivalent to the 4-sphere?
What is the homotopy type of the group of diffeomorphisms of the 4-sphere? ★★★★
Author(s): Smale
Problem 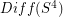 has the homotopy-type of a product space
has the homotopy-type of a product space 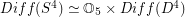 where
where 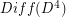 is the group of diffeomorphisms of the 4-ball which restrict to the identity on the boundary. Determine some (any?) homotopy or homology groups of
is the group of diffeomorphisms of the 4-ball which restrict to the identity on the boundary. Determine some (any?) homotopy or homology groups of 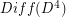 .
.
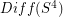 has the homotopy-type of a product space
has the homotopy-type of a product space 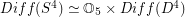 where
where 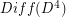 is the group of diffeomorphisms of the 4-ball which restrict to the identity on the boundary. Determine some (any?) homotopy or homology groups of
is the group of diffeomorphisms of the 4-ball which restrict to the identity on the boundary. Determine some (any?) homotopy or homology groups of 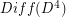 .
. Keywords: 4-sphere; diffeomorphisms
Which compact boundaryless 3-manifolds embed smoothly in the 4-sphere? ★★★
Author(s): Kirby
Problem Determine a computable set of invariants that allow one to determine, given a compact boundaryless 3-manifold, whether or not it embeds smoothly in the 4-sphere. This should include a constructive procedure to find an embedding if the manifold is embeddable.
Keywords: 3-manifold; 4-sphere; embedding

 Drupal
Drupal CSI of Charles University
CSI of Charles University