 login/create account
login/create account
For general 3-manifolds this problem is fairly wide-open. But for some specific families of 3-manifolds it is heavily investigated.
There are two common embedding constructions: (1) obtain your 3-manifold as 0-surgery on a link which is the disjoint union of two smooth slice links. (2) Obtain your 3-manifold as the boundary of a Mazur manifold -- where Mazur manifold is taken to be a contractible 4-manifold constructed as 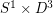 union a 2-handle. In both cases the resulting 3-manifold M embeds smoothly in
union a 2-handle. In both cases the resulting 3-manifold M embeds smoothly in 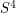 . There are many other embedding constructions but no known "uniform" construction that works for all embeddable 3-manifolds.
. There are many other embedding constructions but no known "uniform" construction that works for all embeddable 3-manifolds.
Since such a 3-manifold would bound two 4-manifolds on either side, the embedding problem is a type of double cobordism problem, and related to issues such as the problem of determining which homology 3-spheres bound homology 4-balls.
The smoothness in the assumption is important. Mike Freedman has proven all homology 3-spheres admit tame topological embeddings into 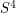 . These embeddings have a less combinatorial nature than smooth embeddings so it is somewhat natural to restrict to the question of smooth embeddings. For example, the Poincare Homology Sphere does not embed smoothly in
. These embeddings have a less combinatorial nature than smooth embeddings so it is somewhat natural to restrict to the question of smooth embeddings. For example, the Poincare Homology Sphere does not embed smoothly in 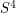 , since it has a non-trivial Rochlin invariant.
, since it has a non-trivial Rochlin invariant.
Bibliography
[B] R. Budney, Embeddings of 3-manifolds in the 4-sphere from the point of view of the  -tetrahedron census, arXiv preprint arXiv:0810.2346
-tetrahedron census, arXiv preprint arXiv:0810.2346
[CH] J.S. Crisp, J.A. Hillman, Embedding Seifert fibred 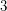 -manifolds and
-manifolds and  -manifolds in
-manifolds in 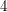 -space,} Proc. London Math Soc. (3) (1998), no. {\bf 3} 685--710.
-space,} Proc. London Math Soc. (3) (1998), no. {\bf 3} 685--710.
[KK] A.~Kawauchi, S.~Kojima, Algebraic classification of linking pairings on 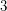 -manifolds, Math. Ann. {\bf 253} (1980), no. 1, 29--42.
-manifolds, Math. Ann. {\bf 253} (1980), no. 1, 29--42.
[FS] R.~Fintushel, R.~Stern, Rational homology cobordisms of spherical space forms, Topology, {\bf 26} no. 3 pp. 385--393, (1987).
[GL] P.M.~Gilmer, C.~Livingston, On embedding 3-manifolds in 4-space, Topology, {\bf 22}, no. 3, pp. 241--252 (1983).
*[K] Kirby, R. Problem list in low-dimensional topology. [http://math.berkeley.edu/~kirby/problems.ps.gz]
[L] R.A.~Litherland, Deforming twist-spun knots, Trans. Amer. Math. Soc. {\bf 250} (1979), 311--331.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University