 login/create account
login/create account
Good Edge Labelings
We say that a graph is good-edge-labeling critical, if it has no good edge labeling, but every proper subgraph has a good edge labeling.
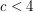 , there is only a finite number of good-edge-labeling critical graphs with average degree less than
, there is only a finite number of good-edge-labeling critical graphs with average degree less than  .
. Let  be a finite undirected simple graph. A good edge labeling of
be a finite undirected simple graph. A good edge labeling of  is an assignment of distinct numbers to the edges such that every cycle has at least two local maxima. (The distinctness of the labels is required only to make the term `local maximum' unambiguous.)
is an assignment of distinct numbers to the edges such that every cycle has at least two local maxima. (The distinctness of the labels is required only to make the term `local maximum' unambiguous.)
Equivalently, a labeling of the edges is good, if for every pair of distinct vertices 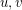 , there is at most one increasing path from
, there is at most one increasing path from  to
to  .
.
Having a good edge labeling is inherited by subgraphs.
It is easy to verify that the graphs 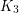 and
and 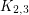 have no good edge labeling. In [ACGH2] an infinite class of graphs without good edge labelings is given, none of whom is a subgraph of the other. In [BFT] contains an example of a minimal graph without good edge labeling which as average degree < 3 (thus refuting an earlier conjecture saying that a good-edge-labeling critical graph with average degree less than three is either
have no good edge labeling. In [ACGH2] an infinite class of graphs without good edge labelings is given, none of whom is a subgraph of the other. In [BFT] contains an example of a minimal graph without good edge labeling which as average degree < 3 (thus refuting an earlier conjecture saying that a good-edge-labeling critical graph with average degree less than three is either 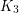 or
or 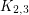 ). In that same paper it is shown that every such graph must have girth at most 4.
). In that same paper it is shown that every such graph must have girth at most 4.
Good edge labeling of graphs was introduced in [BCP] in the context of the so-called Routing and Wavelength Assignment (RWA) problem. The problems above are proposed in [ACGH1] and [ACGH2]. There the algorithmic problem of determining whether a graph has a good edge labeling is shown to be NP-hard. Moreover, the authors also prove that every planar graph with girth at least six has a good edge labeling.
Bibliography
[BCP] J-C. Bermond, M. Cosnard, and S. Pérennes. Directed acyclic graphs with unique path property. Technical report 6932, INRIA, May 2009
[ACGH1] J. Araújo, N. Cohen, F. Giroire, F. Havet. Good edge-labelling of graphs. (English summary) LAGOS'09—V Latin-American Algorithms, Graphs and Optimization Symposium, 275–280, Electron. Notes Discrete Math., 35, Elsevier Sci. B. V., Amsterdam, 2009. MathSciNet
[ACGH2*] J. Araujo, N. Cohen, F. Giroire, and F. Havet. Good edge-labelling of graphs. Research Report 6934, INRIA, 2009.
[BFT] M. Bode, B. Farzad, D.O. Theis. Good edge-labelings and graphs of girth at least 5. (arXiv:1109.1125)
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
First question (almost) solved
Mehrabian, Mitsche, and Pralat showed that any -vertex graph with a good edge-labelling has at most
-vertex graph with a good edge-labelling has at most 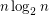 edges, and that for each
edges, and that for each  there is an
there is an  -vertex graphs with a good edge-labelling having
-vertex graphs with a good edge-labelling having 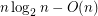 edges.
edges.
http://arxiv.org/abs/1211.2641