 login/create account
login/create account
Havet, Frédéric
Erdős-Posa property for long directed cycles ★★
Conjecture Let 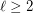 be an integer. For every integer
be an integer. For every integer 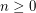 , there exists an integer
, there exists an integer 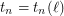 such that for every digraph
such that for every digraph  , either
, either  has a
has a  pairwise-disjoint directed cycles of length at least
pairwise-disjoint directed cycles of length at least 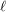 , or there exists a set
, or there exists a set 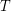 of at most
of at most 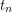 vertices such that
vertices such that 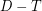 has no directed cycles of length at least
has no directed cycles of length at least 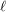 .
.
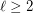 be an integer. For every integer
be an integer. For every integer 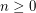 , there exists an integer
, there exists an integer 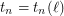 such that for every digraph
such that for every digraph  , either
, either  has a
has a  pairwise-disjoint directed cycles of length at least
pairwise-disjoint directed cycles of length at least 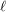 , or there exists a set
, or there exists a set 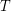 of at most
of at most 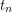 vertices such that
vertices such that 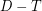 has no directed cycles of length at least
has no directed cycles of length at least 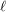 .
. Keywords:
Antidirected trees in digraphs ★★
Author(s): Addario-Berry; Havet; Linhares Sales; Reed; Thomassé
An antidirected tree is an orientation of a tree in which every vertex has either indegree 0 or outdergree 0.
Conjecture Let  be a digraph. If
be a digraph. If  , then
, then  contains every antidirected tree of order
contains every antidirected tree of order  .
.
 be a digraph. If
be a digraph. If  , then
, then  contains every antidirected tree of order
contains every antidirected tree of order  .
. Keywords:
Good Edge Labelings ★★
Author(s): Araújo; Cohen; Giroire; Havet
Question What is the maximum edge density of a graph which has a good edge labeling?
We say that a graph is good-edge-labeling critical, if it has no good edge labeling, but every proper subgraph has a good edge labeling.
Conjecture For every 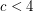 , there is only a finite number of good-edge-labeling critical graphs with average degree less than
, there is only a finite number of good-edge-labeling critical graphs with average degree less than  .
.
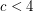 , there is only a finite number of good-edge-labeling critical graphs with average degree less than
, there is only a finite number of good-edge-labeling critical graphs with average degree less than  .
. Keywords: good edge labeling, edge labeling

 Drupal
Drupal CSI of Charles University
CSI of Charles University