 login/create account
login/create account
good edge labeling, edge labeling
Good edge labeling and girth ★★
Author(s): Bode-Farzad-Theis
Conjecture Every graph with large girth has a good edge labeling.
More specifically: there exists a constant  such that every graph with girth at least
such that every graph with girth at least  has a good edge labeling.
has a good edge labeling.
Keywords: good edge labeling, edge labeling
Good Edge Labelings ★★
Author(s): Araújo; Cohen; Giroire; Havet
Question What is the maximum edge density of a graph which has a good edge labeling?
We say that a graph is good-edge-labeling critical, if it has no good edge labeling, but every proper subgraph has a good edge labeling.
Conjecture For every 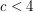 , there is only a finite number of good-edge-labeling critical graphs with average degree less than
, there is only a finite number of good-edge-labeling critical graphs with average degree less than  .
.
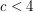 , there is only a finite number of good-edge-labeling critical graphs with average degree less than
, there is only a finite number of good-edge-labeling critical graphs with average degree less than  .
. Keywords: good edge labeling, edge labeling

 Drupal
Drupal CSI of Charles University
CSI of Charles University