 login/create account
login/create account
Complete bipartite subgraphs of perfect graphs
Problem Let  be a perfect graph on
be a perfect graph on  vertices. Is it true that either
vertices. Is it true that either  or
or 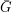 contains a complete bipartite subgraph with bipartition
contains a complete bipartite subgraph with bipartition 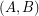 so that
so that 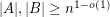 ?
?
 be a perfect graph on
be a perfect graph on  vertices. Is it true that either
vertices. Is it true that either  or
or 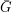 contains a complete bipartite subgraph with bipartition
contains a complete bipartite subgraph with bipartition 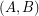 so that
so that 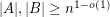 ?
? Every perfect graph on  vertices either has a clique or an independent set of size
vertices either has a clique or an independent set of size 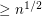 , so weakening the bound on
, so weakening the bound on 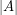 ,
, 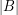 to
to 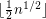 gives a true statement. Jacob Fox [F] has proved that every comparability graph
gives a true statement. Jacob Fox [F] has proved that every comparability graph  on
on  vertices has a complete bipartite subgraph of size
vertices has a complete bipartite subgraph of size 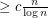 , and (up to the constant) this is best possible.
, and (up to the constant) this is best possible.
Bibliography
[F] J. Fox, A Bipartite Analogue of Dilworth’s Theorem, Order 23 (2006), 197-209.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
Claimed to be solved
In this recent preprint on Paul Seymour's webpage: http://web.math.princeton.edu/~pds/papers/pure5/paper.pdf (not on ArXiv nor published yet)