 login/create account
login/create account
perfect graph
Complete bipartite subgraphs of perfect graphs ★★
Author(s): Fox
Problem Let  be a perfect graph on
be a perfect graph on  vertices. Is it true that either
vertices. Is it true that either  or
or 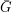 contains a complete bipartite subgraph with bipartition
contains a complete bipartite subgraph with bipartition 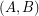 so that
so that 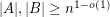 ?
?
 be a perfect graph on
be a perfect graph on  vertices. Is it true that either
vertices. Is it true that either  or
or 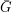 contains a complete bipartite subgraph with bipartition
contains a complete bipartite subgraph with bipartition 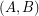 so that
so that 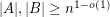 ?
? Keywords: perfect graph
Bounding the chromatic number of graphs with no odd hole ★★★
Author(s): Gyarfas
Conjecture There exists a fixed function 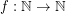 so that
so that 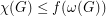 for every graph
for every graph  with no odd hole.
with no odd hole.
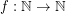 so that
so that 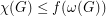 for every graph
for every graph  with no odd hole.
with no odd hole. Keywords: chi-bounded; coloring; induced subgraph; odd hole; perfect graph

 Drupal
Drupal CSI of Charles University
CSI of Charles University