 login/create account
login/create account
Conjecture Denote by 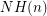 the number of non-Hamiltonian 3-regular graphs of size
the number of non-Hamiltonian 3-regular graphs of size 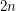 , and similarly denote by
, and similarly denote by 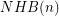 the number of non-Hamiltonian 3-regular 1-connected graphs of size
the number of non-Hamiltonian 3-regular 1-connected graphs of size 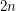 .
.
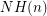 the number of non-Hamiltonian 3-regular graphs of size
the number of non-Hamiltonian 3-regular graphs of size 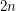 , and similarly denote by
, and similarly denote by 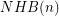 the number of non-Hamiltonian 3-regular 1-connected graphs of size
the number of non-Hamiltonian 3-regular 1-connected graphs of size 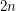 .
.
Is it true that 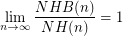 ?
?
A stronger version of this conjecture asks whether it is also the case that 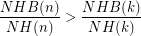 for all
for all 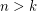 .
.
Experimental data was given by Filar et al [FHN] demonstrating that the strong conjecture is satisfied for all 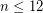 , and with sampled data provided for
, and with sampled data provided for 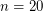 and
and 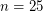 . No further results have been forthcoming.
. No further results have been forthcoming.
The experimental data can be viewed at http://dx.doi.org/10.7151/dmgt.1485
Packers And Movers Chandigarh
Packers And Movers Hyderabad
Packers And Movers Bangalore
Bibliography
[FHN] Jerzy A Filar, Giang T Nguyen, Michael Haythorpe, "A conjecture on the prevalence of cubic bridge graphs", Discussiones Mathematicae Graph Theory 30(1):175--179 (2010).
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University