 login/create account
login/create account
Haythorpe, Michael
Almost all non-Hamiltonian 3-regular graphs are 1-connected ★★
Author(s): Haythorpe
Conjecture Denote by 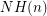 the number of non-Hamiltonian 3-regular graphs of size
the number of non-Hamiltonian 3-regular graphs of size 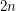 , and similarly denote by
, and similarly denote by 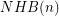 the number of non-Hamiltonian 3-regular 1-connected graphs of size
the number of non-Hamiltonian 3-regular 1-connected graphs of size 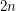 .
.
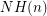 the number of non-Hamiltonian 3-regular graphs of size
the number of non-Hamiltonian 3-regular graphs of size 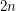 , and similarly denote by
, and similarly denote by 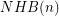 the number of non-Hamiltonian 3-regular 1-connected graphs of size
the number of non-Hamiltonian 3-regular 1-connected graphs of size 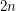 .
.
Is it true that 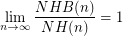 ?
?

 Drupal
Drupal CSI of Charles University
CSI of Charles University