 login/create account
login/create account
Intersection of complete funcoids (Solved)
Conjecture If  ,
,  are complete funcoids (generalized closures) then
are complete funcoids (generalized closures) then 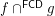 is a complete funcoid (generalized closure).
is a complete funcoid (generalized closure).
 ,
,  are complete funcoids (generalized closures) then
are complete funcoids (generalized closures) then 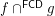 is a complete funcoid (generalized closure).
is a complete funcoid (generalized closure). See Algebraic General Topology for definitions of used concepts.
Below is also a weaker conjecture:
Conjecture If  ,
,  are binary relations then
are binary relations then 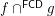 is a binary relation; or equivalently,
is a binary relation; or equivalently, 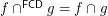 for any binary relations
for any binary relations  and
and  .
.
 ,
,  are binary relations then
are binary relations then 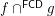 is a binary relation; or equivalently,
is a binary relation; or equivalently, 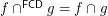 for any binary relations
for any binary relations  and
and  .
. The author has found a counterexample against this weaker conjecture and thus against the main conjecture. The example is 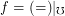 and
and 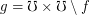 . It is simple to show that
. It is simple to show that 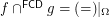 where
where 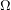 is the Fréchet filter and thus
is the Fréchet filter and thus 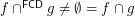 .
.
See the section "Some counter-examples" in the online article "Funcoids and Reloids" for details.
Bibliography
*Victor Porton. Algebraic General Topology
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
Please improve presentation!
Please, provide
1) definitions of the used concepts (to make the statement self-contained)
2) motivation (why this is important, examples, ...)
At the present state, this text is unfortunately not very useful for someone not acquainted with your manuscripts.