 login/create account
login/create account
Conjecture If  ,
,  are complete funcoids (generalized closures) then
are complete funcoids (generalized closures) then 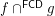 is a complete funcoid (generalized closure).
is a complete funcoid (generalized closure).
 ,
,  are complete funcoids (generalized closures) then
are complete funcoids (generalized closures) then 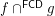 is a complete funcoid (generalized closure).
is a complete funcoid (generalized closure). See Algebraic General Topology for definitions of used concepts.
Below is also a weaker conjecture:
Conjecture If  ,
,  are binary relations then
are binary relations then 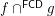 is a binary relation; or equivalently,
is a binary relation; or equivalently, 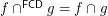 for any binary relations
for any binary relations  and
and  .
.
 ,
,  are binary relations then
are binary relations then 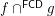 is a binary relation; or equivalently,
is a binary relation; or equivalently, 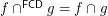 for any binary relations
for any binary relations  and
and  .
. The author has found a counterexample against this weaker conjecture and thus against the main conjecture. The example is 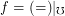 and
and 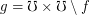 . It is simple to show that
. It is simple to show that 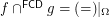 where
where 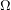 is the Fréchet filter and thus
is the Fréchet filter and thus 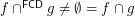 .
.
See the section "Some counter-examples" in the online article "Funcoids and Reloids" for details.
Bibliography
*Victor Porton. Algebraic General Topology
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University