Home » Subject » Graph Theory » Coloring » Vertex coloring

Double-critical graph conjecture

Importance: Medium ✭✭
Author(s): Erdos, Paul
Lovasz, Laszlo
Subject: Graph Theory
» Coloring
» » Vertex coloring
Keywords: coloring
complete graph
Recomm. for undergrads: no
Posted by: DFR
on: January 18th, 2009

A connected simple graph $ G $ is called double-critical, if removing any pair of adjacent vertexes lowers the chromatic number by two.

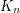Conjecture   $ K_n $ is the only $ n $-chromatic double-critical graph

This conjecture is a special case of a more general problem by Erdos and Lovasz proposed in 1966. It has been independently proven for the case where 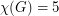$ \chi(G) = 5 $ by Mozhan [3] and Stiebitz [4].

Bibliography

*[1] P. Erdos, Problem 2, in: Theory of Graphs (Proc. Colloq., Tihany, 1966), Academic Press, New York, 1968, p. 361.

[2] F. Chung, R. Graham, Erdos on graphs: His legacy of unsolved problems, A K Peters, Wellesley, Massachusetts, 1998.

[3] N. N. Mozhan, On double critical graphs with the chromatic number five, Metody Diskretb. Anal. 46 (1987) 50-59.

[4] M. Stiebitz, 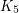$ K_5 $ is the only double-critical $ 5 $-chromatic graph, Discrete Math. 64 (1987) 91-93.


* indicates original appearance(s) of problem.
add new comment

Statement needs connected assumption

On November 30th, 2009 Anonymous says:

G needs to be assumed connected in the statement. Otherwise the disjoint union of K_k and a vertex (say) would be a counterexample.

reply

missing connectivity condition

On May 29th, 2009 Anonymous says:

As it is now the conjecture is false -- take the disjoint union of a clique and a vertex. Just need to add "connected" to the definition of doubly critical.

reply

Comment viewing options

Select your preferred way to display the comments and click "Save settings" to activate your changes.