Does every subcubic triangle-free graph have fractional chromatic number at most 14/5? (Solved)

Importance: Low ✭

Author(s):	Heckman, Christopher C.
	Thomas, Robin

Subject:	Graph Theory
	» Coloring
	» » Vertex coloring

Keywords:

fractional coloring

Recomm. for undergrads: no

Posted	by:	Andrew King
	on:	April 20th, 2011

Solved by:

Zdeněk Dvořák, Jean-Sébastien Sereni, and Jan Volec [DSV]

Conjecture Every triangle-free graph with maximum degree at most 3 has fractional chromatic number at most 14/5.

This conjecture was posed by Heckman and Thomas [HT]. Due to the generalized Petersen graph 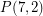$P(7,2)$ , which has 14 vertices and no stable set of size 6, this would be best possible.

The conjecture requires that every triangle-free subcubic graph contains a stable set of size at least 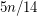$5n/14$ . This was first proved by Staton [S]. The proof was then improved Jones [J]. Griggs and Murphy [GM] gave a linear-time algorithm for finding a stable set of size at least 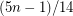$(5n-1)/14$ for any connected subcubic graph, and Heckman and Thomas [HT] have a linear-time algorithm to find a stable set of size at least $5n/14$ .

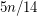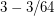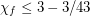Hatami and Zhu [HZ] proved that triangle-free subcubic graphs have fractional chromatic number at most $3-3/64$ . Lu and Peng [LP] improved this bound to $\chi_f \leq 3- 3/43$ .

Bibliography

**[DSV] Z. Dvořák, J.-S. Sereni, and J. Volec, Subcubic triangle-free graphs have fractional chromatic number at most 14/5, arXiv:1301.5296 [math.CO]

[GM] J. Griggs and O. Murphy. Edge density and the independence ratio in triangle-free graphs with maximum degree three. Discrete Math. 152 (1996) 157--170.

[HZ] H. Hatami and X. Zhu. The fractional chromatic number of graphs of maximum degree at most three. SIAM J. Discrete Math. 233 (2001) 233-237.

*[HT] Christopher Carl Heckman and Robin Thomas. A new proof of the independence ratio of triangle-free cubic graphs. Discrete Math. 233 (2001), 233--237.

[J] K. F. Jones. Size and independence in triangle-free graphs with maximum degree three. J. Graph Theory 14 (1990) 525--535.

[LP] L. Lu and X. Peng. The fractional chromatic number of triangle-free graphs with 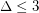$\Delta \leq 3$ .