 login/create account
login/create account
Big Line or Big Clique in Planar Point Sets
Let  be a set of points in the plane. Two points
be a set of points in the plane. Two points  and
and  in
in  are visible with respect to
are visible with respect to  if the line segment between
if the line segment between  and
and  contains no other point in
contains no other point in  .
.
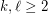 there is an integer
there is an integer  such that every set of at least
such that every set of at least  points in the plane contains at least
points in the plane contains at least  collinear points or
collinear points or  pairwise visible points.
pairwise visible points. The conjecture is trivial for 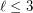 .
.
Kára et al. [KPW] proved the conjecture for 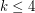 and all
and all  .
.
Addario-Berry et al. [AFKCW] proved the conjecture for 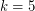 and
and 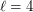 .
.
Abel et al. [ABBCDHKLPW] proved the conjecture for 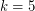 and all
and all  .
.
The conjecture is open for 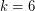 or
or 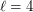 .
.
Note that it is easily proved that for all 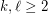 , every set of at least
, every set of at least 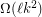 points in the plane contains
points in the plane contains  collinear points or
collinear points or  points with no three collinear [Brass].
points with no three collinear [Brass].
See [Matousek] for related results and questions.
Bibliography
[ABBCDHKLPW] Zachary Abel, Brad Ballinger, Prosenjit Bose, Sébastien Collette, Vida Dujmović, Ferran Hurtado, Scott D. Kominers, Stefan Langerman, Attila Pór, David R. Wood. Every Large Point Set contains Many Collinear Points or an Empty Pentagon, Graphs and Combinatorics 27(1): 47-60, 2011.
[AFKCW] Louigi Addario-Berry, Cristina Fernandes, Yoshiharu Kohayakawa, Jos Coelho de Pina, and Yoshiko Wakabayashi. On a geometric Ramsey-style problem, 2007.
[Brass] Peter Brass. On point sets without k collinear points. In Discrete Geometry, vol. 253 of Monographs and Textbooks in Pure and Applied Mathematics, pp. 185–192. Dekker, New York, 2003.
*[KPW] Jan Kára, Attila Pór, David R. Wood. On the chromatic number of the visibility graph of a set of points in the plane, Discrete and Computational Geometry 34(3):497-506, 2005.
[Matousek] Jiří Matoušek. Blocking visibility for points in general position, Discrete and Computational Geometry 42(2): 219-223, 2009.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
Improved bound in the proof for k=5 and arbitrary l
In their proof of the case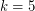 and arbitrary
and arbitrary  , Abel et al. [ABBCDHKLPW] proved a doubly exponential upper bound on the number
, Abel et al. [ABBCDHKLPW] proved a doubly exponential upper bound on the number 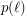 of points that guarantees the occurrence of an
of points that guarantees the occurrence of an  -tuple of collinear points or a
-tuple of collinear points or a  -tuple of points with no other point in their convex hull (an empty pentagon). The upper bound on
-tuple of points with no other point in their convex hull (an empty pentagon). The upper bound on 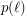 was improved by Barát et al. [BDJPSSVW] to
was improved by Barát et al. [BDJPSSVW] to 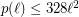 .
.
[BDJPSSVW] János Barát, Vida Dujmović, Gwenaël Joret, Michael S. Payne, Ludmila Scharf, Daria Schymura, Pavel Valtr, and David R. Wood. Empty pentagons in point sets with collinearities, arxiv:1207.3633, 2012.