Discrete Geometry

Big Line or Big Clique in Planar Point Sets ★★

Let $S$ be a set of points in the plane. Two points $v$ and $w$ in $S$ are visible with respect to $S$ if the line segment between $v$ and $w$ contains no other point in $S$ .

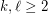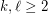Conjecture For all integers $k,\ell\geq2$ there is an integer $n$ such that every set of at least $n$ points in the plane contains at least $\ell$ collinear points or $k$ pairwise visible points.

Keywords: Discrete Geometry; Geometric Ramsey Theory

Posted by David Wood
updated September 25th, 2012

1 comment

Open Problem Garden

Discrete Geometry

Big Line or Big Clique in Planar Point Sets ★★

Navigate

Recent Activity