In their proof of the case and arbitrary , Abel et al. [ABBCDHKLPW] proved a doubly exponential upper bound on the number of points that guarantees the occurrence of an -tuple of collinear points or a -tuple of points with no other point in their convex hull (an empty pentagon). The upper bound on was improved by Barát et al. [BDJPSSVW] to .
[BDJPSSVW] János Barát, Vida Dujmović, Gwenaël Joret, Michael S. Payne, Ludmila Scharf, Daria Schymura, Pavel Valtr, and David R. Wood. Empty pentagons in point sets with collinearities, arxiv:1207.3633, 2012.
Improved bound in the proof for k=5 and arbitrary l
In their proof of the case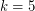 and arbitrary
and arbitrary  , Abel et al. [ABBCDHKLPW] proved a doubly exponential upper bound on the number
, Abel et al. [ABBCDHKLPW] proved a doubly exponential upper bound on the number 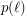 of points that guarantees the occurrence of an
of points that guarantees the occurrence of an  -tuple of collinear points or a
-tuple of collinear points or a  -tuple of points with no other point in their convex hull (an empty pentagon). The upper bound on
-tuple of points with no other point in their convex hull (an empty pentagon). The upper bound on 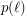 was improved by Barát et al. [BDJPSSVW] to
was improved by Barát et al. [BDJPSSVW] to 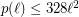 .
.
[BDJPSSVW] János Barát, Vida Dujmović, Gwenaël Joret, Michael S. Payne, Ludmila Scharf, Daria Schymura, Pavel Valtr, and David R. Wood. Empty pentagons in point sets with collinearities, arxiv:1207.3633, 2012.