 login/create account
login/create account
Partitioning
Partitioning the Projective Plane ★★
Author(s): Noel
Throughout this post, by projective plane we mean the set of all lines through the origin in 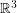 .
.
 of the projective plane is octahedral if all lines in
of the projective plane is octahedral if all lines in  pass through the closure of two opposite faces of a regular octahedron centered at the origin.
pass through the closure of two opposite faces of a regular octahedron centered at the origin.  of the projective plane is weakly octahedral if every set
of the projective plane is weakly octahedral if every set 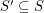 such that
such that 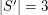 is octahedral.
is octahedral. 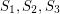 and
and  such that each set
such that each set 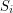 is weakly octahedral. Then each
is weakly octahedral. Then each 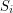 is octahedral.
is octahedral. Keywords: Partitioning; projective plane
2-colouring a graph without a monochromatic maximum clique ★★
 is a non-empty graph containing no induced odd cycle of length at least
is a non-empty graph containing no induced odd cycle of length at least  , then there is a
, then there is a  -vertex colouring of
-vertex colouring of  in which no maximum clique is monochromatic.
in which no maximum clique is monochromatic. Keywords: maximum clique; Partitioning
Convex 'Fair' Partitions Of Convex Polygons ★★
Author(s): Nandakumar; Ramana
Basic Question: Given any positive integer n, can any convex polygon be partitioned into n convex pieces so that all pieces have the same area and same perimeter?
Definitions: Define a Fair Partition of a polygon as a partition of it into a finite number of pieces so that every piece has both the same area and the same perimeter. Further, if all the resulting pieces are convex, call it a Convex Fair Partition.
Questions: 1. (Rephrasing the above 'basic' question) Given any positive integer n, can any convex polygon be convex fair partitioned into n pieces?
2. If the answer to the above is "Not always'', how does one decide the possibility of such a partition for a given convex polygon and a given n? And if fair convex partition is allowed by a specific convex polygon for a give n, how does one find the optimal convex fair partition that minimizes the total length of the cut segments?
3. Finally, what could one say about higher dimensional analogs of this question?
Conjecture: The authors tend to believe that the answer to the above 'basic' question is "yes". In other words they guess: Every convex polygon allows a convex fair partition into n pieces for any n
Keywords: Convex Polygons; Partitioning

 Drupal
Drupal CSI of Charles University
CSI of Charles University