 login/create account
login/create account
Partitioning the Projective Plane
Throughout this post, by projective plane we mean the set of all lines through the origin in 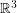 .
.
 of the projective plane is octahedral if all lines in
of the projective plane is octahedral if all lines in  pass through the closure of two opposite faces of a regular octahedron centered at the origin.
pass through the closure of two opposite faces of a regular octahedron centered at the origin.  of the projective plane is weakly octahedral if every set
of the projective plane is weakly octahedral if every set 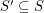 such that
such that 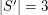 is octahedral.
is octahedral. 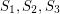 and
and  such that each set
such that each set 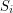 is weakly octahedral. Then each
is weakly octahedral. Then each 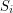 is octahedral.
is octahedral. Also, see the posting on mathoverflow.
There is an equivalent definition of the "weakly octahedral" condition which may be useful.
 of the projective plane is weakly octahedral if for any three lines in
of the projective plane is weakly octahedral if for any three lines in  and any three vectors
and any three vectors 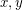 and
and  which span these lines, we have
which span these lines, we have 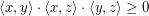 where
where 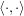 is the standard (dot) inner product on
is the standard (dot) inner product on 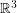 .
. The fact that 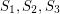 and
and  partition the projective plane seems to be important. Here is an example of a weakly octahedral set that is not octahedral: Fix any vector
partition the projective plane seems to be important. Here is an example of a weakly octahedral set that is not octahedral: Fix any vector  and let
and let  be the set of all lines which are spanned by vectors which meet
be the set of all lines which are spanned by vectors which meet  at an angle strictly less than
at an angle strictly less than 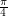 .
.
This question came up while working on another problem posted to this site: Circular colouring the orthogonality graph. It is possible that a solution to the problem stated here can be applied to solve this problem. Moreover, it may be useful in proving that the real orthogonality graph (defined in the other posting) has (essentially) only one proper  -colouring.
-colouring.
Bibliography
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University