 login/create account
login/create account
McDiarmid, Colin
2-colouring a graph without a monochromatic maximum clique ★★
Conjecture If  is a non-empty graph containing no induced odd cycle of length at least
is a non-empty graph containing no induced odd cycle of length at least  , then there is a
, then there is a  -vertex colouring of
-vertex colouring of  in which no maximum clique is monochromatic.
in which no maximum clique is monochromatic.
 is a non-empty graph containing no induced odd cycle of length at least
is a non-empty graph containing no induced odd cycle of length at least  , then there is a
, then there is a  -vertex colouring of
-vertex colouring of  in which no maximum clique is monochromatic.
in which no maximum clique is monochromatic. Keywords: maximum clique; Partitioning
Arc-disjoint directed cycles in regular directed graphs ★★
Author(s): Alon; McDiarmid; Molloy
Conjecture If  is a
is a  -regular directed graph with no parallel arcs, then
-regular directed graph with no parallel arcs, then  contains a collection of
contains a collection of 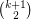 arc-disjoint directed cycles.
arc-disjoint directed cycles.
 is a
is a  -regular directed graph with no parallel arcs, then
-regular directed graph with no parallel arcs, then  contains a collection of
contains a collection of 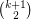 arc-disjoint directed cycles.
arc-disjoint directed cycles. Keywords:
Weighted colouring of hexagonal graphs. ★★
Conjecture There is an absolute constant  such that for every hexagonal graph
such that for every hexagonal graph  and vertex weighting
and vertex weighting 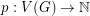 ,
, 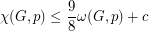
 such that for every hexagonal graph
such that for every hexagonal graph  and vertex weighting
and vertex weighting 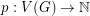 ,
, 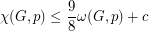
Keywords:

 Drupal
Drupal CSI of Charles University
CSI of Charles University