 login/create account
login/create account
 such that for every hexagonal graph
such that for every hexagonal graph  and vertex weighting
and vertex weighting 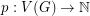 ,
, 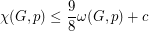
A hexagonal graph is an induced subgraph of the triangular lattice. The triangular lattice 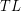 may be described as follows. The vertices are all integer linear combinations
may be described as follows. The vertices are all integer linear combinations 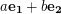 of the two vectors
of the two vectors 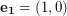 and
and 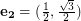 . Two vertices are adjacent when the Euclidean distance between them is 1.
. Two vertices are adjacent when the Euclidean distance between them is 1.
Let  be a graph and
be a graph and 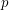 a vertex weighting
a vertex weighting 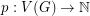 . The weighted clique number of
. The weighted clique number of 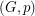 , denoted by
, denoted by 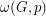 , is the maximum weight of a clique, that is
, is the maximum weight of a clique, that is 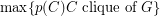 , where
, where 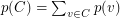 . A
. A  -colouring of a
-colouring of a 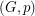 is a mapping
is a mapping 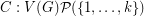 such that for every vertex
such that for every vertex 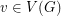 ,
, 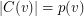 and for all edge
and for all edge 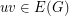 ,
, 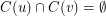 . The chromatic number of
. The chromatic number of 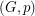 , denoted by
, denoted by 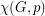 , is the least integer
, is the least integer 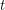 such that
such that 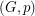 admits a
admits a 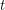 -colouring.
-colouring.
The conjecture would be tight because of 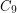 the cycle of length 9. The maximum size of stable set in
the cycle of length 9. The maximum size of stable set in 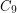 is
is 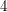 . Thus
. Thus 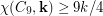 and
and 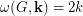 , where
, where 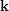 is the all
is the all  function.
function.
McDiarmid and Reed [MR] proved that 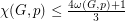 for any hexagonal graph
for any hexagonal graph  and vertex weighting
and vertex weighting 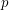 . Havet [H] proved that if a hexagonal graph
. Havet [H] proved that if a hexagonal graph  is triangle-free, then
is triangle-free, then 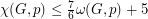 (See also [SV]).
(See also [SV]).
The conjecture would be implied by the following one, where 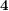 is the all
is the all 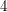 function.
function.
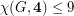 for every hexagonal graph.
for every hexagonal graph. Since 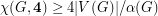 , where
, where 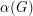 is the stability number (the maximum size of a stable set). A first step to this later conjecture would be to prove the following conjecture of McDiarmid.
is the stability number (the maximum size of a stable set). A first step to this later conjecture would be to prove the following conjecture of McDiarmid.
 be a triangle-free hexagonal graph.
be a triangle-free hexagonal graph. 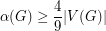
Bibliography
[H] F.Havet. Channel assignment and multicolouring of the induced subgraphs of the triangular lattice. Discrete Mathematics 233:219--231, 2001.
*[MR] C. McDiarmid and B. Reed. Channel assignment and weighted coloring, Networks, 36:114--117, 2000.
[SV] K. S. Sudeep and S. Vishwanathan. A technique for multicoloring triangle-free hexagonal graphs. Discrete Mathematics, 300(1-3), 256--259, 2005.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University