Home » Subject » Graph Theory » Coloring » Edge coloring

Strong edge colouring conjecture

Importance: Medium ✭✭
Author(s): Erdos, Paul
Nesetril, Jaroslav
Subject: Graph Theory
» Coloring
» » Edge coloring
Keywords:
Recomm. for undergrads: no
Posted by: fhavet
on: March 1st, 2013

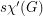A strong edge-colouring of a graph $ G $ is a edge-colouring in which every colour class is an induced matching; that is, any two vertices belonging to distinct edges with the same colour are not adjacent. The strong chromatic index $ s\chi'(G) $ is the minimum number of colours in a strong edge-colouring of $ G $.

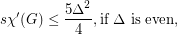
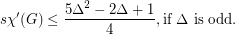
Conjecture   $$s\chi'(G) \leq \frac{5\Delta^2}{4}, \text{if $\Delta$ is even,}$$ $$s\chi'(G) \leq \frac{5\Delta^2-2\Delta +1}{4},&\text{if $\Delta$ is odd.}$$

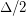The conjectured bounds would be sharp. When $ D $ is even, expanding each vertex of a $ 5 $-cycle into a stable set of size $ \Delta/2 $ yields such a graph with 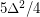$ 5\Delta^2/4 $ edges in which the largest induced matching has size 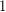$ 1 $. A similar construction achieves the bound when $ \Delta $ is odd.

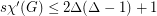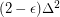Greedy colouring the edges yields $ s\chi'(G) \leq 2\Delta(\Delta-1)+1 $. Using probabilistic methods, Molloy and Reed~[MoRe97] proved that there is a positive constant $ \epsilon $ such that, for sufficiently large $ \Delta $, every graph with maximum degree $ \Delta $ has strong chromatic index at most $ (2-\epsilon)\Delta^2 $.

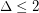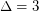The greedy bound proves the conjecture for $ \Delta \leq 2 $. For $ \Delta =3 $, the conjectured bound of 10 was proved independently by Hor\'ak, He, and Trotter[HHT] and by Andersen [A]. For 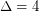$ \Delta=4 $, the conjectured bound is 20, and Cranston [C] proved that 22 colours suffice.

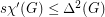For a bipartite graph $ G $, Faudree et al. [FGST] conjectured that $ s\chi'(G)\leq \Delta^2(G) $. This is implied by the stronger conjecture due to Kaiser.

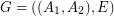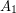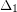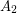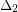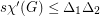Conjecture   Let $ G=((A_1,A_2),E) $ be a bipartite graph such that every vertex in $ A_1 $ has degree at most $ \Delta_1 $ and every vertex in $ A_2 $ has degree at most $ \Delta_2 $. Then $ s\chi'(G)\leq \Delta_1\Delta_2 $.

Bibliography

[A] L. D. Andersen. The strong chromatic index of a cubic graph is at most 10. Discrete Math., 108(1-3):231--252, 1992.

[C] D. W. Cranston. Strong edge-coloring of graphs with maximum degree 4 using 22 colors. Discrete Math., 306(21):2772--2778, 2006.

[FGST] R. J. Faudree, A. Gyárfás, R. H. Schelp, and Zs. Tuza. Induced matchings in bipartite graphs. Discrete Math., 78(1-2):83--87, 1989.

[HHT] P. Horák, Q. He, and W. T. Trotter. Induced matchings in cubic graphs. J. Graph Theory, 17(2):151--160, 1993.


* indicates original appearance(s) of problem.
add new comment