Home » Subject » Topology

Sticky Cantor sets

Importance: Medium ✭✭
Author(s):
Subject: Topology
Keywords: Cantor set
Recomm. for undergrads: no
Posted by: porton
on: February 6th, 2011
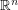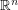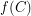Conjecture   Let $ C $ be a Cantor set embedded in $ \mathbb{R}^n $. Is there a self-homeomorphism $ f $ of $ \mathbb{R}^n $ for every $ \epsilon $ greater than $ 0 $ so that $ f $ moves every point by less than $ \epsilon $ and $ f(C) $ does not intersect $ C $? Such an embedded Cantor set for which no such $ f $ exists (for some $ \epsilon $) is called "sticky". For what dimensions $ n $ do sticky Cantor sets exist?

I borrowed this conjecture from this forum thread.

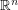Certainly I understand this conjecture wrongly: $ C $ is a subset of a line segment. Consider a homeomorphism which moves all points of $ \mathbb{R}^n $ orthogonally to this line segment by 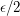$ \epsilon/2 $. This would be a solution of this problem. Obviously it is not what is meant.

Indeed I submit the problem to OPG as is in the hope that somebody will correct my wrong understanding and adjust the formulation to not be misunderstood as by me.

Bibliography



* indicates original appearance(s) of problem.
add new comment

Misunderstanding

On July 29th, 2011 Anonymous says:

Your misunderstanding comes from the definition of a Cantor set. A Cantor set is a set homeomorphic to the usual middle-thirds Cantor set. In general it does not have to lie on a line segment.

reply

M

On April 10th, 2012 Anonymous says:

"embedded" does not imply that it is still a subset of the line. It just says that it's one-to-one and a homeomorphism with the image. The conjecture requires to prove that there exists a Cantor which cannot be separated from itself, so showing an example where it can be separated is not relevant.

reply

Comment viewing options

Select your preferred way to display the comments and click "Save settings" to activate your changes.