 login/create account
login/create account
Cantor set
Sticky Cantor sets ★★
Author(s):
Conjecture Let  be a Cantor set embedded in
be a Cantor set embedded in 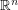 . Is there a self-homeomorphism
. Is there a self-homeomorphism  of
of 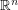 for every
for every  greater than
greater than  so that
so that  moves every point by less than
moves every point by less than  and
and 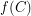 does not intersect
does not intersect  ? Such an embedded Cantor set for which no such
? Such an embedded Cantor set for which no such  exists (for some
exists (for some  ) is called "sticky". For what dimensions
) is called "sticky". For what dimensions  do sticky Cantor sets exist?
do sticky Cantor sets exist?
 be a Cantor set embedded in
be a Cantor set embedded in 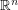 . Is there a self-homeomorphism
. Is there a self-homeomorphism  of
of 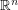 for every
for every  greater than
greater than  so that
so that  moves every point by less than
moves every point by less than  and
and 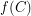 does not intersect
does not intersect  ? Such an embedded Cantor set for which no such
? Such an embedded Cantor set for which no such  exists (for some
exists (for some  ) is called "sticky". For what dimensions
) is called "sticky". For what dimensions  do sticky Cantor sets exist?
do sticky Cantor sets exist? Keywords: Cantor set

 Drupal
Drupal CSI of Charles University
CSI of Charles University