 login/create account
login/create account
Separators in string graphs (Solved)
 edges has a separator of size
edges has a separator of size 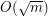 .
. Consider a graph 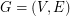 with vertex weights
with vertex weights 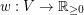 . A separator in
. A separator in  is a set
is a set  of vertices such that there is a partition
of vertices such that there is a partition 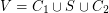 of the vertices with no edge going between
of the vertices with no edge going between 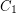 and
and 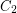 and with
and with 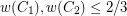 . The size of the separator
. The size of the separator  is the number of vertices of
is the number of vertices of  .
.
The result holds for planar graphs (which form a subclass of string graphs) by the Lipton-Tarjan theorem~[LT]. The best known upper bound for string graphs is currently 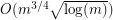 from~[FP].
from~[FP].
Update: Solved by James Lee [Lee].
Bibliography
*[FPT] Jacob Fox, János Pach, Csaba D. Tóth: Intersection patterns of curves, J. London Math. Soc., to appear
[FP] Jacob Fox, János Pach A separator theorem for string graphs and its applications, Combinatorics, Probability and Computing, to appear.
[LT] Richard J. Lipton, Robert Endre Tarjan: A separator theorem for planar graphs, SIAM Journal on Applied Mathematics 36 (1979), 177-–189.
[Lee] James R. Lee. Separators in region intersection graphs, 2016.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
Jiri Matousek has almost
Jiri Matousek has almost solved this problem. He proves a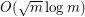 upper bound in "Near-optimal separators in string graphs" at arXiv:1302.6482.
upper bound in "Near-optimal separators in string graphs" at arXiv:1302.6482.