 login/create account
login/create account
Pach, János
Odd-cycle transversal in triangle-free graphs ★★
Author(s): Erdos; Faudree; Pach; Spencer
Conjecture If  is a simple triangle-free graph, then there is a set of at most
is a simple triangle-free graph, then there is a set of at most 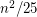 edges whose deletion destroys every odd cycle.
edges whose deletion destroys every odd cycle.
 is a simple triangle-free graph, then there is a set of at most
is a simple triangle-free graph, then there is a set of at most 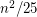 edges whose deletion destroys every odd cycle.
edges whose deletion destroys every odd cycle. Keywords:
Are different notions of the crossing number the same? ★★★
Problem Does the following equality hold for every graph  ?
? ![\[ \text{pair-cr}(G) = \text{cr}(G) \]](/files/tex/8cece1e00bb0e9fc122e0a5cad0dab2681cf33a4.png)
 ?
? ![\[ \text{pair-cr}(G) = \text{cr}(G) \]](/files/tex/8cece1e00bb0e9fc122e0a5cad0dab2681cf33a4.png)
The crossing number 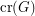 of a graph
of a graph  is the minimum number of edge crossings in any drawing of
is the minimum number of edge crossings in any drawing of  in the plane. In the pairwise crossing number
in the plane. In the pairwise crossing number 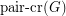 , we minimize the number of pairs of edges that cross.
, we minimize the number of pairs of edges that cross.
Keywords: crossing number; pair-crossing number

 Drupal
Drupal CSI of Charles University
CSI of Charles University