 login/create account
login/create account
 ?
? ![\[ \text{pair-cr}(G) = \text{cr}(G) \]](/files/tex/8cece1e00bb0e9fc122e0a5cad0dab2681cf33a4.png)
The crossing number 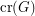 of a graph
of a graph  is the minimum number of edge crossings in any drawing of
is the minimum number of edge crossings in any drawing of  in the plane. In the pairwise crossing number
in the plane. In the pairwise crossing number 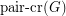 , we minimize the number of pairs of edges that cross.
, we minimize the number of pairs of edges that cross.
Obviously we have 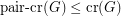 .
.
The problem was first posed by Pach and Tóth in~[PT], who first spotted the possibility that the pairwise crossing number might be different from the crossing number. They proved 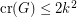 for graphs with pairwise crossing number
for graphs with pairwise crossing number  , which was later improved by Valtr~[V05] to
, which was later improved by Valtr~[V05] to 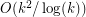 and by Tóth~[T08] to
and by Tóth~[T08] to 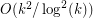 .
.
Bibliography
*[PT] János Pach, Géza Tóth, Which crossing number is it anyway?, Journal of Combinatorial Theory Series B 80 (2000), no. 2, 225--246. MathSciNet
[V05] Pavel Valtr, On the pair-crossing number, Combinatorial and computational geometry, 52 (2005), 569--575. MathSciNet
[T08] Géza Tóth, Note on the pair-crossing number and the odd-crossing number, Discrete Comput. Geom., 39 (2008), no. 4, 791--799. MathSciNet
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University