 login/create account
login/create account
Point sets with no empty pentagon
Let  be a finite set of points in the plane (not necessarily in general position). Two points
be a finite set of points in the plane (not necessarily in general position). Two points 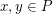 are visible if the line segment
are visible if the line segment 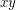 contains no other point in
contains no other point in  . The visibility graph of
. The visibility graph of  has vertex set
has vertex set  , where two vertices are adjacent if and only if they are visible. An empty pentagon in
, where two vertices are adjacent if and only if they are visible. An empty pentagon in  consists of 5 points in
consists of 5 points in  that are the vertices of a strictly convex pentagon whose interior contains none of the points in
that are the vertices of a strictly convex pentagon whose interior contains none of the points in  .
.
Consider the following three closely related classes of point sets:
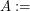 point sets with no empty pentagon (called a 5-hole),
point sets with no empty pentagon (called a 5-hole),
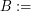 point sets with no 5 pairwise visible points,
point sets with no 5 pairwise visible points,
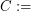 point sets whose visibility graph is 4-colourable.
point sets whose visibility graph is 4-colourable.
By definition, 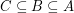 , and it is easy to show that
, and it is easy to show that 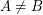 and
and 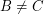 .
.
A key example of a point set in 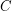 is the planar grid (intersected with a convex set so that it is finite): colour each grid point
is the planar grid (intersected with a convex set so that it is finite): colour each grid point 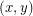 by
by 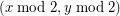 . If
. If 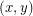 and
and 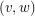 receive the same colour then
receive the same colour then 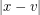 and
and 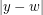 are both even, and thus the midpoint of
are both even, and thus the midpoint of 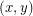 and
and 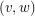 is a blocker. Hence the visibility graph of the grid is 4-colourable. [This result and proof is folklore.] Many other examples of point sets in these classes can be found in the references.
is a blocker. Hence the visibility graph of the grid is 4-colourable. [This result and proof is folklore.] Many other examples of point sets in these classes can be found in the references.
Consider the following open problems:
- \item Classify the point sets in
 ,
, 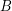 , or
, or 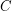
(i.e. list all examples; this is easy for point sets with no empty quadrilateral, or no 4 pairwise visible points).
\item Does the visibility graph of every point set in
 have bounded chromatic number?
have bounded chromatic number?\item Does the visibility graph of every point set in
 have bounded clique number?
have bounded clique number?\item Does the visibility graph of every point set in
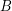 have bounded chromatic number?
have bounded chromatic number? Kára-Pór-Wood gave an example of a point set in  with chromatic number
with chromatic number  .
.
Bibliography
Z. Abel, B. Ballinger, P. Bose, S. Collette, V. Dujmovic, F. Hurtado, S. D. Kominers, S. Langerman, A. Pór, D. R. Wood. Every large point set contains many collinear points or an empty pentagon, Graphs and Combinatorics 27(1):47-60, 2011.
Eppstein, David. Happy endings for flip graphs. J. Computational Geometry 1(1):3-28, 2010. MathSciNet
Kára, Jan; Pór, Attila; Wood, David R. On the chromatic number of the visibility graph of a set of points in the plane. Discrete Comput. Geom. 34(3):497-506, 2005. MathSciNet
Pfender, Florian. Visibility graphs of point sets in the plane. Discrete Comput. Geom. 39 (2008), no. 1-3, 455–459. MathSciNet
Rabinowitz, Stanley. Consequences of the pentagon property. Geombinatorics 14:208-220, 2005.
* indicates original appearance(s) of problem.
Problem 2 solved
Since the chromatic number is always equal or greater than the clique number, the chromatic number of the visibility graph of sets in A is also unbounded.
Cibulka, Kyncl and Valtr have also indirectly solved problem 2.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
Problem 3 solved
Cibulka, Kyncl and Valtr have solved problem 3. They constructed point sets with no empty pentagon, and whose visibility graph has arbitrarily large clique number.
Josef Cibulka, Jan Kyncl and Pavel Valtr: On planar point sets with the pentagon property, Proc. SoCG 2013, pp. 81-90. http://dl.acm.org/citation.cfm?id=2462406