login/create account
Partition of Complete Geometric Graph into Plane Trees
Conjecture Every complete geometric graph with an even number of vertices has a partition of its edge set into plane (i.e. non-crossing) spanning trees.
For a set 
of 
points in the plane with no three collinear, the complete geometric graph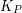 
has vertex set and edge set consisting of the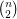 
straight line-segments between each pair of points in .
Since each subtree of 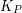has at most 
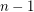edges, every partition of 
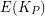into subtrees has at least 
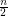parts. The conjecture asks for such a partition into exactly 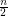subtrees, such that in addition, no two edges in each subtree cross.
It is folklore that the conjecture is true if is in convex partition. In fact, the edge set of the complete convex graph can be partitioned into plane Hamiltonian paths. Bose et al. [BHRW] characterised all possible partitions of the complete convex graph into plane spanning trees. Bose et al. [BHRW] also proved that every complete geometric graph on vertices can be partitioned into at most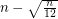 
plane subtrees.
I heard about this conjecture from Ferran Hurtado in 2003, but the problem is much older than that.
Bibliography
[BHRW] Prosenjit Bose, Ferran Hurtado, Eduardo Rivera-Campo, David R. Wood. Partitions of complete geometric graphs into plane trees, Computational Geometry: Theory & Applications 34(2):116-125, 2006. MathSciNet
* indicates original appearance(s) of problem.
Drupal
CSI of Charles University
This conjecture is false
This conjecture has recently been disproved, see arXiv:2108.05159 and arXiv:2112.08456.