Home » Subject » Graph Theory

Number of Cliques in Minor-Closed Classes

Importance: Medium ✭✭
Author(s): Wood, David R.
Subject: Graph Theory
Keywords: clique
graph
minor
Recomm. for undergrads: no
Posted by: David Wood
on: October 12th, 2009
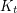Question   Is there a constant $ c $ such that every $ n $-vertex $ K_t $-minor-free graph has at most 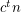$ c^tn $ cliques?

Here a clique is a (not neccessarily maximal) set of pairwise adjacent vertices in a graph.

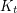See [RW, NSTW] for early bounds on the number of cliques. Wood [W] proved that the number of cliques in an $ n $-vertex $ K_t $-minor-free graph is at most 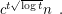$ c^{t\sqrt{\log t}}n\enspace. $ Fomin et al. [FOT] improved this bound to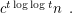 $ c^{t\log\log t}n\enspace. $

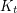These results are based on the fact that every $ n $-vertex $ K_t $-minor-free graph has at most 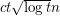$ ct\sqrt{\log t}n $ edges. This bound is tight for certain random graphs. So it is reasonable to expect that random graphs might also provide good lower bounds on the number of cliques.

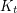Update 2014: Choongbum Lee and Sang-il Oum [LO] recently answered this question in the affirmative, and even proved it for excluded subdivisions. In particular, they proved that every $ n $-vertex graph with no $ K_t $-subdivision has at most 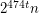$ 2^{474t}n $ cliques and also at most 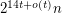$ 2^{14t+o(t)}n $ cliques.

The question now is to determine the minimum constant. Wood [W] proved a lower bound of 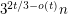$ 3^{2t/3-o(t)}n $ using an appropriate sized complete graph minus a perfect matching. The same graph gives a lower bound of 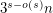$ 3^{s-o(s)}n $ on the number of cliques in a graph with no 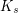$ K_s $ subdivision.

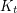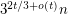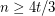Update (2019): Fox and Wei [FW] have proved that every graph on $ n $ vertices with no $ K_t $-minor has at most $ 3^{2t/3+o(t)}n $ cliques. This bound is tight for $ n \geq 4t/3 $.

Bibliography

[FOT] Fedor V. Fomin, Sang il Oum, and Dimitrios M. Thilikos. Rank-width and tree-width of $ H $-minor-free graphs, European J. Combin. 31 (7), 1617–1628, 2010.

[NSTW] Serguei Norine, Paul Seymour, Robin Thomas, Paul Wollan. Proper minor-closed families are small. J. Combin. Theory Ser. B, 96(5):754--757, 2006.

[RW] Bruce Reed and David R. Wood. Fast separation in a graph with an excluded minor. In 2005 European Conf. on Combinatorics, Graph Theory and Applications (EuroComb '05), vol. AE of Discrete Math. Theor. Comput. Sci. Proceedings, pp. 45--50. 2005.

* [W] David R. Wood. On the maximum number of cliques in a graph. Graphs Combin., 23(3):337--352, 2007.

[LO] Choongbum Lee and Sang-il Oum. Number of cliques in graphs with forbidden minor, 2014.

[FW] Jacob Fox, Fan Wei. On the number of cliques in graphs with a forbidden minor


* indicates original appearance(s) of problem.
add new comment