 login/create account
login/create account
Monadic second-order logic with cardinality predicates
The problem concerns the extension of Monadic Second Order Logic (over a binary relation representing the edge relation) with the following atomic formulas:
- \item
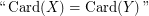 \item
\item 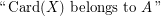
where  is a fixed recursive set of integers.
is a fixed recursive set of integers.
Let us fix  and a closed formula
and a closed formula 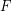 in this language.
in this language.
Conjecture Is it true that the validity of 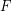 for a graph
for a graph  of tree-width at most
of tree-width at most  can be tested in polynomial time in the size of
can be tested in polynomial time in the size of  ?
?
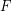 for a graph
for a graph  of tree-width at most
of tree-width at most  can be tested in polynomial time in the size of
can be tested in polynomial time in the size of  ?
? Bibliography
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University