 login/create account
login/create account
FMT03-Bedlewo
Monadic second-order logic with cardinality predicates ★★
Author(s): Courcelle
The problem concerns the extension of Monadic Second Order Logic (over a binary relation representing the edge relation) with the following atomic formulas:
- \item
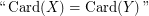 \item
\item 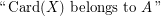
where  is a fixed recursive set of integers.
is a fixed recursive set of integers.
Let us fix  and a closed formula
and a closed formula 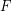 in this language.
in this language.
Conjecture Is it true that the validity of 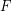 for a graph
for a graph  of tree-width at most
of tree-width at most  can be tested in polynomial time in the size of
can be tested in polynomial time in the size of  ?
?
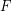 for a graph
for a graph  of tree-width at most
of tree-width at most  can be tested in polynomial time in the size of
can be tested in polynomial time in the size of  ?
? Keywords: bounded tree width; cardinality predicates; FMT03-Bedlewo; MSO
Fixed-point logic with counting ★★
Author(s): Blass
Question Can either of the following be expressed in fixed-point logic plus counting:
- \item Given a graph, does it have a perfect matching, i.e., a set
 of edges such that every vertex is incident to exactly one edge from
of edges such that every vertex is incident to exactly one edge from  ? \item Given a square matrix over a finite field (regarded as a structure in the natural way, as described in [BGS02]), what is its determinant?
? \item Given a square matrix over a finite field (regarded as a structure in the natural way, as described in [BGS02]), what is its determinant? Keywords: Capturing PTime; counting quantifiers; Fixed-point logic; FMT03-Bedlewo

 Drupal
Drupal CSI of Charles University
CSI of Charles University