 login/create account
login/create account
Graphs with a forbidden induced tree are chi-bounded
Say that a family 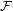 of graphs is
of graphs is 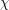 -bounded if there exists a function
-bounded if there exists a function  so that every
so that every 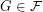 satisfies
satisfies 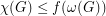 .
.
 , the family of graphs with no induced subgraph isomorphic to
, the family of graphs with no induced subgraph isomorphic to  is
is 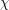 -bounded.
-bounded. This deep conjecture remains open despite considerable effort. Note that the conjecture would be false were the graph  to be permitted to contain a cycle, since then the class would admit graphs of high girth (where
to be permitted to contain a cycle, since then the class would admit graphs of high girth (where 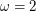 ) and high chromatic number.
) and high chromatic number.
It is an easy exercise to prove this conjecture in the special case when  is either a path or a star, but things get difficult from here. Kierstead and Penrice solved the special case when
is either a path or a star, but things get difficult from here. Kierstead and Penrice solved the special case when  has radius 2, and Kierstead and Zhu solved the special case when
has radius 2, and Kierstead and Zhu solved the special case when  has radius 3 and has the property that every vertex incident with the center vertex has degree 2.
has radius 3 and has the property that every vertex incident with the center vertex has degree 2.
Scott proved that the class of graphs which exclude all subdivisions of a fixed tree  as induced subgraphs are
as induced subgraphs are 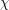 -bounded. It follows from this that Gyarfas's conjecture also holds for subdivisions of stars.
-bounded. It follows from this that Gyarfas's conjecture also holds for subdivisions of stars.
Bibliography
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University