 login/create account
login/create account
Generalised Empty Hexagon Conjecture
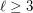 there is an integer
there is an integer 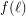 such that every set of at least
such that every set of at least 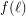 points in the plane contains
points in the plane contains  collinear points or an empty hexagon.
collinear points or an empty hexagon. Here an empty hexagon in a set of points  consists of a subset
consists of a subset 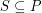 of six points in convex position with no other point in
of six points in convex position with no other point in  in the convex hull of
in the convex hull of  . The
. The 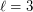 case of the conjecture (that is, for point sets in general position) was an outstanding open problem for many years, until its solution by Gerken [G] and Nicolas [N]. Valtr [V] found a simple proof.
case of the conjecture (that is, for point sets in general position) was an outstanding open problem for many years, until its solution by Gerken [G] and Nicolas [N]. Valtr [V] found a simple proof.
Bibliography
[G] Tobias Gerken. Empty Convex Hexagons in Planar Point Sets, Discrete Comput Geom (2008) 39:239–272, MathSciNet
[N] Carlos M. Nicolas. The Empty Hexagon Theorem, Discrete Comput Geom 38:389–397 (2007), MathSciNet.
[V] Pavel Valtr, On Empty Hexagons, in: J. E. Goodman, J. Pach, and R. Pollack, Surveys on Discrete and Computational Geometry, Twenty Years Later, Contemp. Math. 453, AMS, 2008, pp. 433-441.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University