 login/create account
login/create account
Exponential Algorithms for Knapsack
The famous 0-1 Knapsack problem is: Given 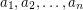 and
and  integers, determine whether or not there are
integers, determine whether or not there are 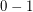 values
values 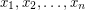 so that
so that 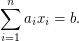 The best known worst-case algorithm runs in time
The best known worst-case algorithm runs in time 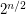 times a polynomial in
times a polynomial in  . Is there an algorithm that runs in time
. Is there an algorithm that runs in time 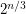 ?
?
Bibliography
[SS] Richard Schroeppel and Adi Shamir. A T=O(2n/2), S=O(2n/4) algorithm for certain NP-complete problems, SIAM J. Comput. 10 (1981), no. 3, 456--464.
* indicates original appearance(s) of problem.
Updates
Publications from 2010 on this topic: Pseudopolynomial algorithm with only polynomial space: Daniel Lokshtanov and Jesper Nederlof: "Saving Space by Algebraization". To appear in the proceedings of ACM Symposium on Theory of Computing (STOC 2010).
Fast knapsack: Nick Howgrave-Graham and Antoine Joux: "New Generic Algorithms for Hard Knapsacks". To appear in the proceedings of EUROCRYPT 2010 The running time is O^*(2^0.311 n), which is faster than the question posted here.
Obviously, the question could become: find a lower constant than 0.311.
0-1 knapsack
I do not know how to determine the run time but I have an algorithm based on dynamic programming which solves the problem more efficiently than a simple search but not in polynomial time!
I have implemented the procedure as a Java program and tried to express it as a flow chart. Files for both of these are available at; www.cybase.co.uk/wlcs/Software.html
although at the moment the website is down.
I have contacted the ISP to try and restore it.
This appears to be answered
see paper at http://www.joux.biz/publications/Knapsacks.pdf and rjlipton's blog post about it at http://rjlipton.wordpress.com/2010/02/05/a-2010-algorithm-for-the-knapsack-problem/
of course, this is an open ended question, there is still room for better algorithms.
A solution has been announced
A (randomized, probably heuristic) algorithm has been announced to solve this problem in time close to 2^(0.311 n), at the ESC 2010 seminar.
For details, see: https://cryptolux.org/ESC/Antoine_Joux
Subset sum or 0-1?
When your values - your a_n - can be negative, and your b (the goal) is zero, then it's called "subset sum". If the a_n are non-negative (i.e., some of the a's may be zero), the b is positive, and the choice is to either exclude (0) or include (1) one "copy" of each value, then it's a "0-1 knapsack" problem. Usually, but not always, a knapsack problem has components with multiple values, and the goal is a minimax problem: maximize the a's, while minimizing the c's.
It's always darkest, just after the lights go out.
0-1 Knapsack?
I know this problem as subset sum and not as 0-1 knapsack.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
References
Solving this problem in pseudopolynomial time with polynomial space: Daniel Lokshtanov and Jesper Nederlof: "Saving Space by Algebraization". To appear in the proceedings of ACM Symposium on Theory of Computing (STOC 2010).
The next reference solves this problem (even general knapsack, I believe). An 2^{0.311 n} Algorithm: Nick Howgrave-Graham and Antoine Joux : "A new generic algorithm for hard knapsacks". To appear in the proceedings of EUROCRYPT 2010.
However, the problem might be easily adjusted to "find an algorithm that takes O(2^{c n}) time, where c < 0.311", etc etc.