 login/create account
login/create account
Exponential-time algorithm
Algorithm for graph homomorphisms ★★
Author(s): Fomin; Heggernes; Kratsch
Question
Is there an algorithm that decides, for input graphs  and
and  , whether there exists a homomorphism from
, whether there exists a homomorphism from  to
to  in time
in time 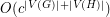 for some constant
for some constant  ?
?
Keywords: algorithm; Exponential-time algorithm; homomorphism
Exponential Algorithms for Knapsack ★★
Author(s): Lipton
Conjecture
The famous 0-1 Knapsack problem is: Given 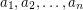 and
and  integers, determine whether or not there are
integers, determine whether or not there are 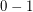 values
values 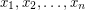 so that
so that 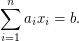 The best known worst-case algorithm runs in time
The best known worst-case algorithm runs in time 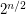 times a polynomial in
times a polynomial in  . Is there an algorithm that runs in time
. Is there an algorithm that runs in time 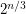 ?
?
Keywords: Algorithm construction; Exponential-time algorithm; Knapsack

 Drupal
Drupal CSI of Charles University
CSI of Charles University