 login/create account
login/create account
| Importance: High ✭✭✭ |
| Author(s): |
| Subject: | Number Theory |
| » Analytic Number Theory |
| Keywords: | constant |
| Euler | |
| irrational | |
| Mascheroni | |
| rational | |
| transcendental |
| Recomm. for undergrads: no |
| Posted | by: | Juggernaut |
| on: | July 19th, 2011 |
Let 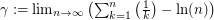 . The number
. The number 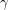 has not been proved algebraic or transcendental. In fact, it is not even known whether
has not been proved algebraic or transcendental. In fact, it is not even known whether 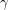 is irrational.
is irrational.
Euler-Masqueroni contant
If n = 2^k then log(n) is irrational. But Sum{1/k} is ever rational . Then Sum{1/k} - Log(n) is ever irrational.. Ludovicus