 login/create account
login/create account
Coloring and immersion
 , every (loopless) graph
, every (loopless) graph  with
with 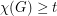 immerses
immerses 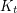 .
. Let  be a graph and let
be a graph and let 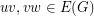 . The operation of deleting the edges
. The operation of deleting the edges 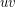 and
and  and then adding a new edge between
and then adding a new edge between  and
and  is called a split. We say that a graph
is called a split. We say that a graph  immerses a graph
immerses a graph  if a graph isomorphic to
if a graph isomorphic to  may be obtained from
may be obtained from  by repeatedly making splits and deleting vertices and edges.
by repeatedly making splits and deleting vertices and edges.
The graph containment relations of minor and topological minor have been thoroughly studied with respect to graph coloring. In particular, there are two famous conjectures: Hajos conjectured that every graph with chromatic number 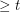 contains a subdivision of the complete graph
contains a subdivision of the complete graph 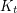 as a subgraph. Hadwiger conjectured that every graph with chromatic number
as a subgraph. Hadwiger conjectured that every graph with chromatic number 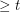 contains
contains 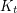 as a minor. While Hajos' Conjecture is false for
as a minor. While Hajos' Conjecture is false for 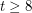 (indeed it is actually false on average), Hadwiger's Conjecture remains open, and is one of the outstanding problems in Graph Theory.
(indeed it is actually false on average), Hadwiger's Conjecture remains open, and is one of the outstanding problems in Graph Theory.
On the other hand, the relationship between graph coloring and immersions seems to have been largely ignored until Abu-Khzam and Langston made the above conjecture. In addition to formulating this conjecture, they proved it for 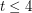 and showed that a minimal counterexample to it must be 4-connected and
and showed that a minimal counterexample to it must be 4-connected and  -edge-connected. Recently, DeVos, Kawarabayashi, Mohar, and Okamura have resolved the conjecture for
-edge-connected. Recently, DeVos, Kawarabayashi, Mohar, and Okamura have resolved the conjecture for 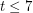 .
.
Bibliography
* Faisal N. Abu-Khzam and Michael A. Langston, Graph Coloring and the Immersion Order
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University