 login/create account
login/create account
Circular choosability of planar graphs
Let 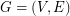 be a graph. If
be a graph. If  and
and 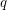 are two integers, a
are two integers, a 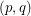 -colouring of
-colouring of  is a function
is a function  from
from 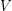 to
to 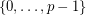 such that
such that 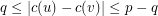 for each edge
for each edge 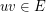 . Given a list assignment
. Given a list assignment  of
of  , i.e.~a mapping that assigns to every vertex
, i.e.~a mapping that assigns to every vertex  a set of non-negative integers, an
a set of non-negative integers, an  -colouring of
-colouring of  is a mapping
is a mapping 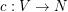 such that
such that 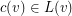 for every
for every 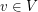 . A list assignment
. A list assignment  is a
is a  -
-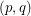 -list-assignment if
-list-assignment if 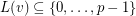 and
and 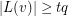 for each vertex
for each vertex 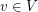 . Given such a list assignment
. Given such a list assignment  , the graph G is
, the graph G is 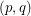 -
- -colourable if there exists a
-colourable if there exists a 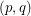 -
- -colouring
-colouring  , i.e.
, i.e.  is both a
is both a 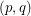 -colouring and an
-colouring and an  -colouring. For any real number
-colouring. For any real number 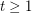 , the graph
, the graph  is
is  -
-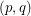 -choosable if it is
-choosable if it is 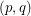 -
- -colourable for every
-colourable for every  -
-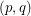 -list-assignment
-list-assignment  . Last,
. Last,  is circularly
is circularly  -choosable if it is
-choosable if it is  -
-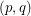 -choosable for any
-choosable for any  ,
, 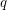 . The circular choosability (or circular list chromatic number or circular choice number) of G is
. The circular choosability (or circular list chromatic number or circular choice number) of G is 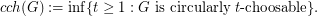
The problem was first posed in 2003 by Mohar (Problem 4 of link*) who suggested the answer should be between 4 and 5.
Some time later, Havet, Kang, Müller, and Sereni [HKMS] showed that in fact the answer is somewhere between 6 and 8. The upper bound extends a celebrated planar choosability proof due to Thomassen [T]. The lower bound is by way of an elementary, though rather large, construction.
Bibliography
[HKMS] F. Havet, R. J. Kang, T. Müller, and J.-S. Sereni. Circular choosability. J. Graph Theory 61 (2009), no. 4, 241--270.
[T] C. Thomassen. Every planar graph is 5-choosable. J. Combinatorial Theory B 62 (1994) 180--181
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University