 login/create account
login/create account
Chromatic Number of Common Graphs
A graph  is common if the sum of the number of copies of
is common if the sum of the number of copies of  in a graph
in a graph  and the number in the complement of
and the number in the complement of  is asymptotically minimised by taking
is asymptotically minimised by taking  to be a random graph (see [HHKNR] for a formal definition).
to be a random graph (see [HHKNR] for a formal definition).
Goodman proved that 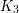 is common [G]. Erdös [E] conjectured that every complete graph is common. Later, this conjecture was extended to all graphs by Burr and Rosta [BR]. Sidorenko [S89] disproved Burr and Rosta’s conjecture by showing that a triangle with a pendant edge is not common. Conjectures of Erdös and Simonovits [ES] and Sidorenko [S91,S93] imply that every bipartite graph is common. Disproving the first conjecture of Erdös, Thomason proved that
is common [G]. Erdös [E] conjectured that every complete graph is common. Later, this conjecture was extended to all graphs by Burr and Rosta [BR]. Sidorenko [S89] disproved Burr and Rosta’s conjecture by showing that a triangle with a pendant edge is not common. Conjectures of Erdös and Simonovits [ES] and Sidorenko [S91,S93] imply that every bipartite graph is common. Disproving the first conjecture of Erdös, Thomason proved that 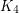 is not common [T]. More generally, Jagger, Šťovíček and Thomason proved that no common graph contains
is not common [T]. More generally, Jagger, Šťovíček and Thomason proved that no common graph contains 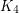 as a subgraph [JST]. The 5-wheel is an example of a 4-chromatic common graph [HHKNR].
as a subgraph [JST]. The 5-wheel is an example of a 4-chromatic common graph [HHKNR].
Bibliography
[BR] Burr, S. A. and Rosta, V. On the Ramsey multiplicities of graphs: Problems and recent results. J. Graph Theory 4 (1980) 347–361.
[E] Paul Erdös, On the number of complete subgraphs contained in certain graphs. Magyar Tud. Akad. Mat. Kutato ́ Int. Ko ̈zl. 7 (1962) 459–464.
[ES] Paul Erdös and Miklós Simonovits (1984) Cube-supersaturated graphs and related problems. In Progress in Graph Theory: Waterloo, Ont., 1982, Academic Press, pp. 203–218.
*[HHKNR] H. Hatami, J. Hladký, D. Kráľ, S. Norine, A. Razborov: Non-three-colorable common graphs exist, Combinatorics, Probability and Computing 21 (2012), 734–742.
[JST] Jagger, Chris; Šťovíček, Pavel; Thomason, Andrew. Multiplicities of subgraphs. Combinatorica 16 (1996) 123–141.
[S89] Sidorenko, A. Cycles in graphs and functional inequalities. Mat. Zametki 46 (1989) 72–79, 104.
[S91] Sidorenko, A. Inequalities for functionals generated by bipartite graphs. Diskret. Mat. 3 (1991) 50–65.
[S93] Sidorenko, A. A correlation inequality for bipartite graphs. Graphs Combin. 9 (1993) 201–204.
[T] Thomason, Andrew. A disproof of a conjecture of Erdo ̋s in Ramsey theory, J. London Math. Soc. (2) 39 (1989) 246–255.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University