Home » Subject » Graph Theory

Sidorenko's Conjecture

Importance: High ✭✭✭
Author(s): Sidorenko, A.
Subject: Graph Theory
Keywords: density problems
extremal combinatorics
homomorphism
Recomm. for undergrads: no
Posted by: Jon Noel
on: October 10th, 2019
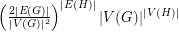Conjecture   For any bipartite graph $ H $ and graph $ G $, the number of homomorphisms from $ H $ to $ G $ is at least $ \left(\frac{2|E(G)|}{|V(G)|^2}\right)^{|E(H)|}|V(G)|^{|V(H)|} $.

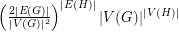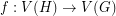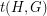A homomorphism from a graph $ H $ to a graph $ G $ is a mapping $ f:V(H)\to V(G) $ which preserves edges. Given graphs $ H $ and $ G $, the homomorphism density of $ H $ in $ G $, denoted $ t(H,G) $, is the probability that a random function 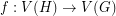$ f:V(H)\to V(G) $ is a homomorphism. That is,

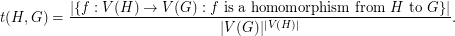
$$t(H,G)=\frac{\left|\left\{f: V(H)\to V(G): f\text{ is a homomorphism from }H\text{ to }G\right\}\right|}{|V(G)|^{|V(H)|}}.$$

In this language, Sidorenko's Conjecture says that, if $ H $ is bipartite, then every graph $ G $ satisfies

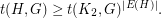
$$t(H,G)\geq t(K_2,G)^{|E(H)|}.$$

There are lots of results on Sidorenko's Conjecture; rather than listing them all here, we encourage the reader to see the references of the recent paper [CL].

Related problems

Chromatic Number of Common Graphs

Bibliography

[CL] David Conlon and Joonkyung Lee: Sidorenko's conjecture for blow-ups, submitted.


* indicates original appearance(s) of problem.
add new comment