 login/create account
login/create account
Chowla's cosine problem
Problem Let 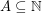 be a set of
be a set of  positive integers and set
positive integers and set ![\[m(A) = - \min_x \sum_{a \in A} \cos(ax).\]](/files/tex/7a772ebd0b7fd98eeab7fda3a5e9674b1dc4c984.png) What is
What is  ?
?
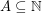 be a set of
be a set of  positive integers and set
positive integers and set ![\[m(A) = - \min_x \sum_{a \in A} \cos(ax).\]](/files/tex/7a772ebd0b7fd98eeab7fda3a5e9674b1dc4c984.png) What is
What is  ?
? It is easy to see that 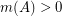 , since the average value of the sum of the cosines is zero. Bourgain [B] proved that
, since the average value of the sum of the cosines is zero. Bourgain [B] proved that 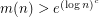 for some
for some 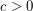 and
and  sufficiently large. Recently, Ruzsa [R] tightened this argument, proving that
sufficiently large. Recently, Ruzsa [R] tightened this argument, proving that 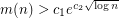 where
where 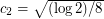 . The proof utilizes a clever manipulation of norms to reveal a (somewhat surprising) additive structure to the problem.
. The proof utilizes a clever manipulation of norms to reveal a (somewhat surprising) additive structure to the problem.
It seems the only known upper bound is 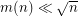 .
.
Bibliography
[B] J. Bourgain, Sur le minimum d'une somme de cosinus, Acta Arith. 45 (1986), 381--389. MathSciNet
*[C] S. Chowla, Some applications of a method of A. Selberg. J. Reine Angew. Math. 217 (1965) 128--132. MathSciNet
[R] I.Z. Ruzsa, Negative values of cosine sums. Acta Arith. 111 (2004), no. 2, 179--186. MathSciNet
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University