 login/create account
login/create account
Another conjecture about reloids and funcoids
Definition 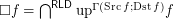 for reloid
for reloid  .
.
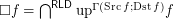 for reloid
for reloid  .
. Conjecture 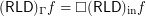 for every funcoid
for every funcoid  .
.
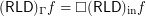 for every funcoid
for every funcoid  .
. Note: it is known that 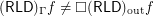 (see below mentioned online article).
(see below mentioned online article).
It's used notation from Algebraic General Topology draft book, modified by this note about new notation for a future version of this book.
Bibliography
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University