 login/create account
login/create account
A path 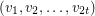 in a vertex-coloured graph
in a vertex-coloured graph  is repetitively coloured if
is repetitively coloured if 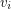 and
and 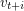 receive the same colour for
receive the same colour for 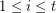 . A colouring of
. A colouring of  is nonrepetitive if no path is repetitively coloured. The nonrepetitive chromatic number of a graph
is nonrepetitive if no path is repetitively coloured. The nonrepetitive chromatic number of a graph  is the minimum number of colours in a nonrepetitive colouring of
is the minimum number of colours in a nonrepetitive colouring of  .
.
For example, every path is nonrepetitively 3-colourable [T], every tree is nonrepetitively 4-colourable [BGKNP], every outerplanar graphs is nonrepetitively 12-colourable [KP], every graph of treewidth  is nonrepetitively
is nonrepetitively 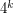 -colourable [KP], and every graph of maximum degree
-colourable [KP], and every graph of maximum degree  is
is 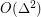 colourable [AGHR,DJKW].
colourable [AGHR,DJKW].
The best known upper bound on the nonrepetitive chromatic number of  -vertex planar graphs is
-vertex planar graphs is 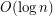 [DFJW]. The best lower bound is 11, due to Pascal Ochem [DFJW].
[DFJW]. The best lower bound is 11, due to Pascal Ochem [DFJW].
More generally, it is open whether graphs with bounded genus or graphs in a fixed minor-closed class have bounded nonrepetitive chromatic number. For such graphs classes, a 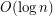 upper bound is known [DMW].
upper bound is known [DMW].
Update [2019]: This problem has been solved [DEJWW]. The authors prove that every planar graph is nonrepetitively 768-colourable. More generally, they prove that graphs of bounded Euler genus, graphs excluding a fixed minor, and graphs excluding a fixed topological minor have bounded nonrepetitive chromatic number.
Bibliography
*[AGHR] Noga Alon, Jarosław Grytczuk, Mariusz Hałuszczak, Oliver Riordan. Nonrepetitive colorings of graphs. Random Structures Algorithms, 21(3-4):336–346, 2002. MathSciNet.
[BGKNP] B. Brešar, J. Grytczuk, S. Klavžar, S. Niwczyk, I. Peterin. Nonrepetitive colorings of trees. Discrete Math., 307(2):163–172, 2007. MathSciNet.
[DFJW] V. Dujmović, F. Frati, G. Joret, D. R. Wood. Nonrepetitive colourings of planar graphs with 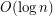 colours, Electronic J. Combinatorics 20.1:P51, 2013.
colours, Electronic J. Combinatorics 20.1:P51, 2013.
[DJKW] V. Dujmović, G. Joret, J. Kozik, D. R. Wood. Nonrepetitive colouring via entropy compression, Combinatorica, to appear.
[DMW] V. Dujmović, P. Morin, D. R. Wood. Layered separators in minor-closed graph classes with applications. J. Combinatorial Theory Series B 127:111–147, 2017.
[KP] André Kündgen, Michael Pelsmajer. Nonrepetitive colorings of graphs of bounded tree-width. Discrete Math., 308(19):4473–4478, 2008.
[T] Axel Thue. Uber unendliche Zeichenreihen. Norske Vid. Selsk. Skr. I. Mat. Nat. Kl. Christiania, 7:1-22, 1906.
[DEJWW] Vida Dujmović, Louis Esperet, Gwenaël Joret, Bartosz Walczak, David R. Wood. Planar graphs have bounded nonrepetitive chromatic number, 2019.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University