 login/create account
login/create account
 is the adjacency matrix of a
is the adjacency matrix of a  -regular graph, then there is a symmetric signing of
-regular graph, then there is a symmetric signing of  (i.e. replace some
(i.e. replace some 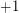 entries by
entries by 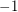 ) so that the resulting matrix has all eigenvalues of magnitude at most
) so that the resulting matrix has all eigenvalues of magnitude at most 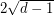 .
. A graph  is a
is a  -lift of a graph
-lift of a graph  if there is a
if there is a  -to-
-to-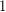 map
map 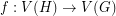 which is locally injective in the sense that the restriction of
which is locally injective in the sense that the restriction of  to the neighbourhood of every vertex is an injection. We can construct a random
to the neighbourhood of every vertex is an injection. We can construct a random  -lift of
-lift of  with vertex set
with vertex set 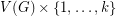 by adding a (uniformly chosen) random matching between
by adding a (uniformly chosen) random matching between 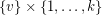 and
and 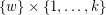 whenever
whenever 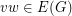 . If
. If  is a
is a  -lift of
-lift of  , then every eigenvalue of
, then every eigenvalue of  will also be an eigenvalue of
will also be an eigenvalue of  , but in addition
, but in addition  will have
will have 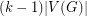 new eigenvalues. There has been considerable interest and investigation into the behaviour of these new eigenvalues for a random
new eigenvalues. There has been considerable interest and investigation into the behaviour of these new eigenvalues for a random  -lift, since it is expected that they should generally be small in magnitude. In particular, if
-lift, since it is expected that they should generally be small in magnitude. In particular, if  is a Ramanujan graph (a
is a Ramanujan graph (a  -regular graph for which all nontrivial eigenvalues are at most
-regular graph for which all nontrivial eigenvalues are at most 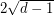 ) it may be possible to construct a new Ramanujan graph by taking a suitable
) it may be possible to construct a new Ramanujan graph by taking a suitable  -lift of
-lift of  . A series of increasingly strong results have shown that a random
. A series of increasingly strong results have shown that a random  -lift of a
-lift of a  -regular Ramanujan graph will have all new eigenvalues at most
-regular Ramanujan graph will have all new eigenvalues at most 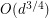 (Friedman [F]),
(Friedman [F]), 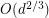 (Linial and Pruder [LP]) and
(Linial and Pruder [LP]) and 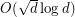 (Lubetzky, Sudakov, and Vu [LSV]).
(Lubetzky, Sudakov, and Vu [LSV]).
An interesting paper of Bilu and Linial [BL] investigates 2-lifts of graphs. Let  be a graph and let
be a graph and let  be a 2-lift of
be a 2-lift of  with vertex set
with vertex set 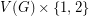 as above. Every eigenvector of
as above. Every eigenvector of  extends naturally to an eigenvector of
extends naturally to an eigenvector of  which is constant on each fiber (set of the form
which is constant on each fiber (set of the form 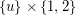 ). Thus, we may assume that all of the new eigenvalues are associated with eigenvectors which sum to zero on each fiber. So, each of these new eigenvectors is completely determined by its behaviour on
). Thus, we may assume that all of the new eigenvalues are associated with eigenvectors which sum to zero on each fiber. So, each of these new eigenvectors is completely determined by its behaviour on 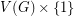 . Now we assign a signature
. Now we assign a signature 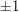 to each edge of
to each edge of  to form a signed graph
to form a signed graph 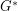 by assigning each edge
by assigning each edge 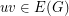 for which
for which 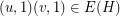 a sign of
a sign of 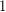 and every other edge of
and every other edge of  sign
sign 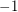 . It is straightforward to verify that the restriction of any new eigenvector of
. It is straightforward to verify that the restriction of any new eigenvector of  to
to 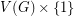 will then be an eigenvector of
will then be an eigenvector of 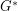 . Thus, the above conjecture is equivalent to the conjecture that every
. Thus, the above conjecture is equivalent to the conjecture that every  -regular graph has a
-regular graph has a  -lift so that all new eigenvalues have magnitude at most
-lift so that all new eigenvalues have magnitude at most 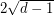 . Furthermore, a positive solution to this conjecture for
. Furthermore, a positive solution to this conjecture for  -regular Ramanujan graphs would yield families of
-regular Ramanujan graphs would yield families of  -regular expanders.
-regular expanders.
Bibliography
*[BL] Y. Bilu, N. Linial, Lifts, discrepancy and nearly optimal spectral gap, Combinatorica 26 (5) (2006) 495–519. MathSciNet
[F] J. Friedman, Relative expanders or weakly relatively Ramanujan graphs, Duke Math. J. 118 (1) (2003) 19–35. MathSciNet
[LP] N. Linial, D. Puder, Word maps and spectra of random graph lifts, Random Structures Algorithms 37 (1) (2010) 100–135. MathSciNet
[LSV] E. Lubetzky, B. Sudakov, V Vu, Spectra of lifted Ramanujan graphs. Adv. Math. 227 (2011), no. 4, 1612–1645. MathSciNet
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University