 login/create account
login/create account
Bilu, Yonatan
Signing a graph to have small magnitude eigenvalues ★★
Conjecture If  is the adjacency matrix of a
is the adjacency matrix of a  -regular graph, then there is a symmetric signing of
-regular graph, then there is a symmetric signing of  (i.e. replace some
(i.e. replace some 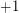 entries by
entries by 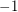 ) so that the resulting matrix has all eigenvalues of magnitude at most
) so that the resulting matrix has all eigenvalues of magnitude at most 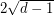 .
.
 is the adjacency matrix of a
is the adjacency matrix of a  -regular graph, then there is a symmetric signing of
-regular graph, then there is a symmetric signing of  (i.e. replace some
(i.e. replace some 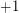 entries by
entries by 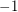 ) so that the resulting matrix has all eigenvalues of magnitude at most
) so that the resulting matrix has all eigenvalues of magnitude at most 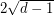 .
. Keywords: eigenvalue; expander; Ramanujan graph; signed graph; signing

 Drupal
Drupal CSI of Charles University
CSI of Charles University